级数收敛例题

陶哲轩又发新论文了！

这也是时隔一年，他再次独立发表新论文。（arXiv显示上一篇独作论文发表时间是在去年2月）

这篇新论文依旧与陶哲轩钻研的数论领域有关。

它证明了著名数学家埃尔德什·帕尔（Erdős Pál）提出的一个交错素数级数猜想，在哈代-李特尔伍德素数k元组猜想成立的条件下，是成立的。

（当然，哈代-李特尔伍德素数k元组猜想也是一个悬而未解的猜想，因此这项研究只是部分证明，并没有完全解决）

这项研究，还用到了他在几年前与合作者共同提出的一个素数随机模型。

一起来看看。

证明了什么样的猜想？

核心来说，这篇新论文要证明的，是埃尔德什提出的一个关于交错素数级数收敛性的猜想。

这个猜想与一个长这样的交错级数有关，其中pn是第n个素数：

但交错级数并不一定收敛，因此需要具体级数具体判断，这次陶哲轩证明的就是交错级数中的一个特殊类型，即an是素数pn的倒数，这个级数是收敛的。

不过，还有个前提条件——在哈代-李特尔伍德素数k元组猜想成立的条件下。

哈代-李特尔伍德素数k元组猜想，由英国科学家哈代和李特尔伍德提出，它预测了给定差值集合的k个素数出现的频率。

猜想认为，存在两个绝对常数ε>0和C>0，对于所有x≥10、所有k≤(log log x)^5、和所有由不同整数h1,…,hk组成的k元组：

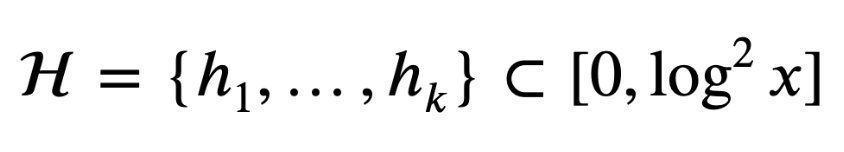
使得这个式子成立：

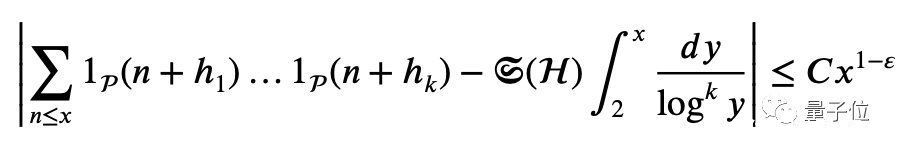
不过，这个猜想至今尚未解决。

这次陶哲轩直接在假设它成立的基础上，证明了交错素数级数收敛性猜想的成立。整个过程大约可以分为四步：

首先，基于Van der Corput差分定理来降低素数计数间隔的长度。

由于证明这个猜想，实际上需要估计区间[1,x]内素数个数的奇偶性分布，因此使用差分定理的目的，能将它转化为仅考虑较短区间内素数个数奇偶性的问题。

转化为这个问题之后，实际上就能用哈代-李特尔伍德素数k元组猜想来证明问题成立。

因此，接下来论文在假设哈代-李特尔伍德素数k元组猜想成立的基础上，估计了短区间内k个素数的概率。

然后，陶哲轩使用几年前与两位数学家William Banks和Kevin Ford共同建立的随机素数模型，来建模素数分布。

最后基于这个模型建立的分布证明猜想。

这篇博客发出后不久，就有网友赶来点赞，表示自己也在从用另一种方法尝试解决这个猜想：

One More Thing

值得一提的是，2004年陶哲轩和本·格林（Ben Joseph Green）提出的著名格林-陶定理，也是基于埃尔德什·帕尔（Erdős Pál）另一个更著名的等差数列猜想而来。

其中，埃尔德什等差数列猜想如下：

格林-陶定理进一步将猜想范围缩小到他们研究的素数范围内，相当于埃尔德什等差数列猜想的一个“特例”：

埃尔德什为解决这个等差数列猜想悬赏了5000美元。

这些年除了陶哲轩以外，也有不少数学家致力于它的研究，例如Thomas Bloom和Olof Sisask。他们在2020年，证明了整数无穷数列一定包含长度至少为三的等差数列，将这个问题又向前推进了一步。

感兴趣的小伙伴们可以挑战一下了（手动狗头）

新论文地址：

参考链接：

— 完 —

量子位 QbitAI · 头条号签约

宦扶霄4953高数中关于级数的问题.若已知一般项为nAn的级数收敛.证明:一般项为An的级数也收敛. -
羿廖裕18916544062 ______[答案] 用Dirichlet判别法: an=nan*(1/n),级数(nan)收敛,数列1/n是递减趋于0的数列,由Dirichlet判别法知道级数(an)收敛.

宦扶霄4953一道大学级数题,正项级数收敛的充分必要条件是:它的部分和数列有界部分和数列有界就能推得 正项级数收敛? -
羿廖裕18916544062 ______[答案] 正项级数每一项都是大于等于0,那么部分和数列就是单调递增,再加上条件有界,根据单调递增有界数列极限必存在准则,就知道这个正项级数的部分和极限存在,即收敛

宦扶霄4953判断级数的敛散性,若级数收敛,求和1):1/2+3/4+5/6+7/8…2):(1/2+1/3)+(1/4+1/9)+(1/8+1/27)+… -
羿廖裕18916544062 ______[答案] 1)该级数发散.∵(2n-1)/(2n)当n趋于无穷时等于1. 2)该级数收敛.当n趋于无穷时,(1/2)^n、(1/3)^n都趋于0, 原式=1/2+(1/2)²+(1/2)³+……+(1/3)+(1/3)²+(1/3)³+…… =(1-0)+(1-0) =2

宦扶霄4953如何证明 ln n/n^(4/3)级数收敛 -
羿廖裕18916544062 ______[答案] 考虑级数1/n^(7/6),该级数收敛 由于lim[lnn/n^(4/3)]/(1/n^(7/6)] =lim[lnn/n^(1/6)] =lim6/n^(1/6)=0故原级数收敛

宦扶霄4953若级数 ∞ n=它un收敛于s,则级数&n七sp; ∞ n=它(un+un+它)( ) -
羿廖裕18916544062 ______[选项] A. 收敛于2s B. 收敛于2s+u1 C. 收敛于2s-u1 D. 发散

宦扶霄4953【无穷级数】正项级数收敛的证明已知正项级数∑an,如何判断∑a2n也收敛?注:其中n和2n均为下标. -
羿廖裕18916544062 ______[答案] 用比较定理呗,构造一个新级数,b_{2n-1}=0,b_{2n}=a_{2n}.于是∑b_n被收敛级数∑a_n所界定,自然也收敛

宦扶霄4953级数收敛若级数(U2n - 1+U2n)发散,则级数Un发散,n趋于无穷,其中2n - 1和2n为下标该如何证明上述表达正确 -
羿廖裕18916544062 ______[答案] 级数(U2n-1+U2n)发散,那n趋于无穷时,∑U2n-1+U2n=2∑Un, 都趋向于无穷,那级数Un自然是发散的

宦扶霄4953求助几道高数题~~1.根据级数收敛于发散的定义判别收敛性:[1/(1*3) ]+[1/(3*5)] +[1/(5*7)]+….+[1/(2n - 1)(2n+1)]2.判别下列级数收敛性(1) - (8/9)+(8^2)/(9^2) - ... -
羿廖裕18916544062 ______[答案] 1、Sn = ∑1/[(2n-1)(2n+1)] = 1/2-1/2(2n+1)limSn = lim[1/2-1/2(2n-1)] = 1/2所以级数∑1/[(2n-1)(2n+1)] 收敛2、1)∑(8/9)^n =∑1/(9/8)^n为p>1的p级数,收敛,所以∑(-1)^n(8/9)^n绝对收敛,因此收敛2)∑1/2^n与∑1...

宦扶霄49531.下列级数收敛的是: -
羿廖裕18916544062 ______[选项] A. ∑(-1)的n-1次方乘以n/n+1 B. ∑3^n/2^n C. ∑(-1)的n-1次方除以n D. ∑1/根号n 2.级数∑(n^2/3^n)x^2n-1的收敛区间为?

宦扶霄4953求级数并证明级数收敛的例题 -
羿廖裕18916544062 ______ 严格说来,都要写上的,才能保证绝对不会被判错误.因为幂级数只有在收敛域内才能与和函数相等!式也是这个道理.