导数五步法画函数图像10个函数示意图应用举例之一
\n\n
\n\n
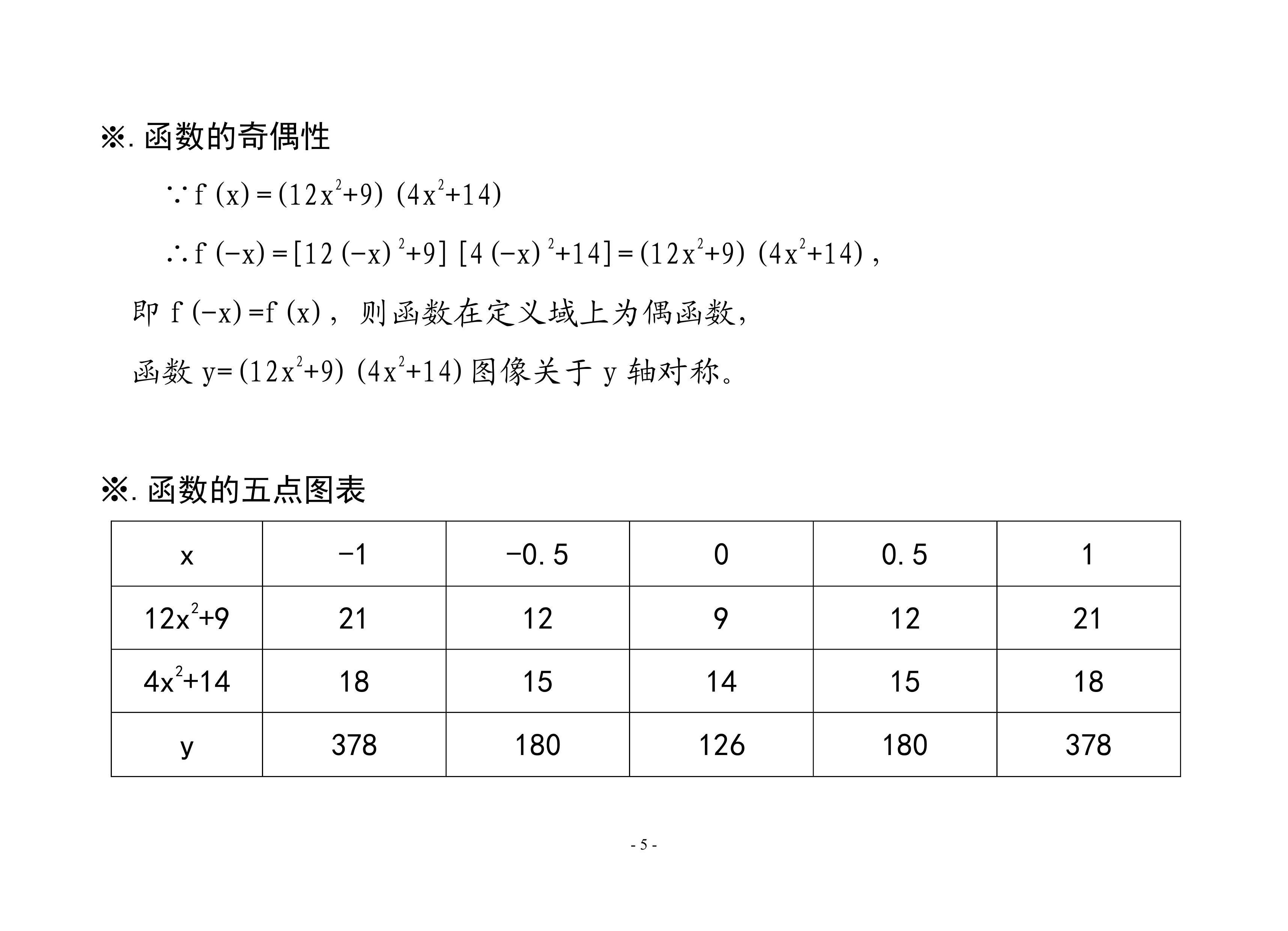
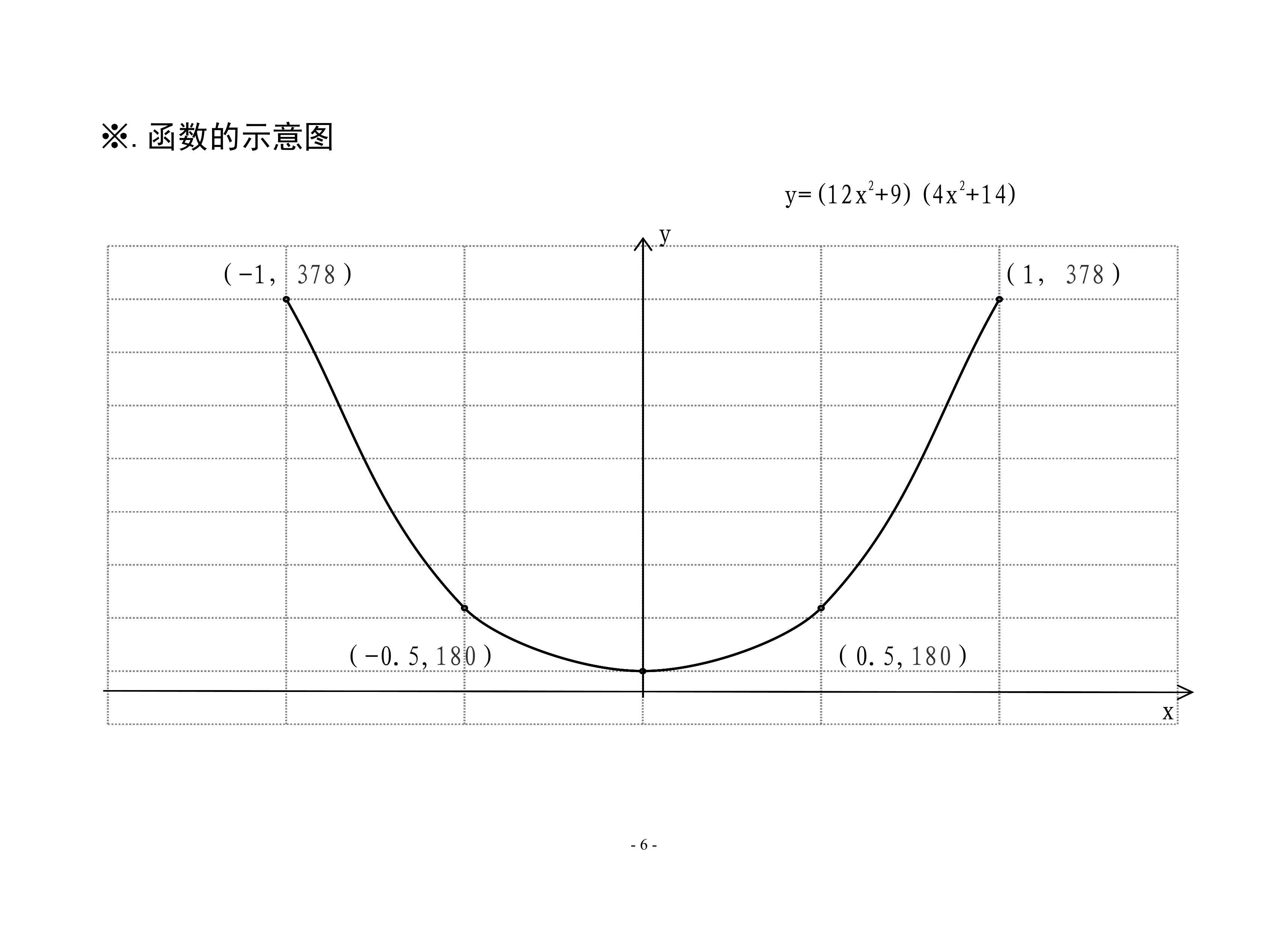
1.函数y=(12x2+9)(4x2+14)的图像示意图:介绍函数的定义域、单调性、凸凹性、极限等性质及五点图表,并通过导数知识计算函数的单调和凸凹区间,简要画出示意图。
\n\n
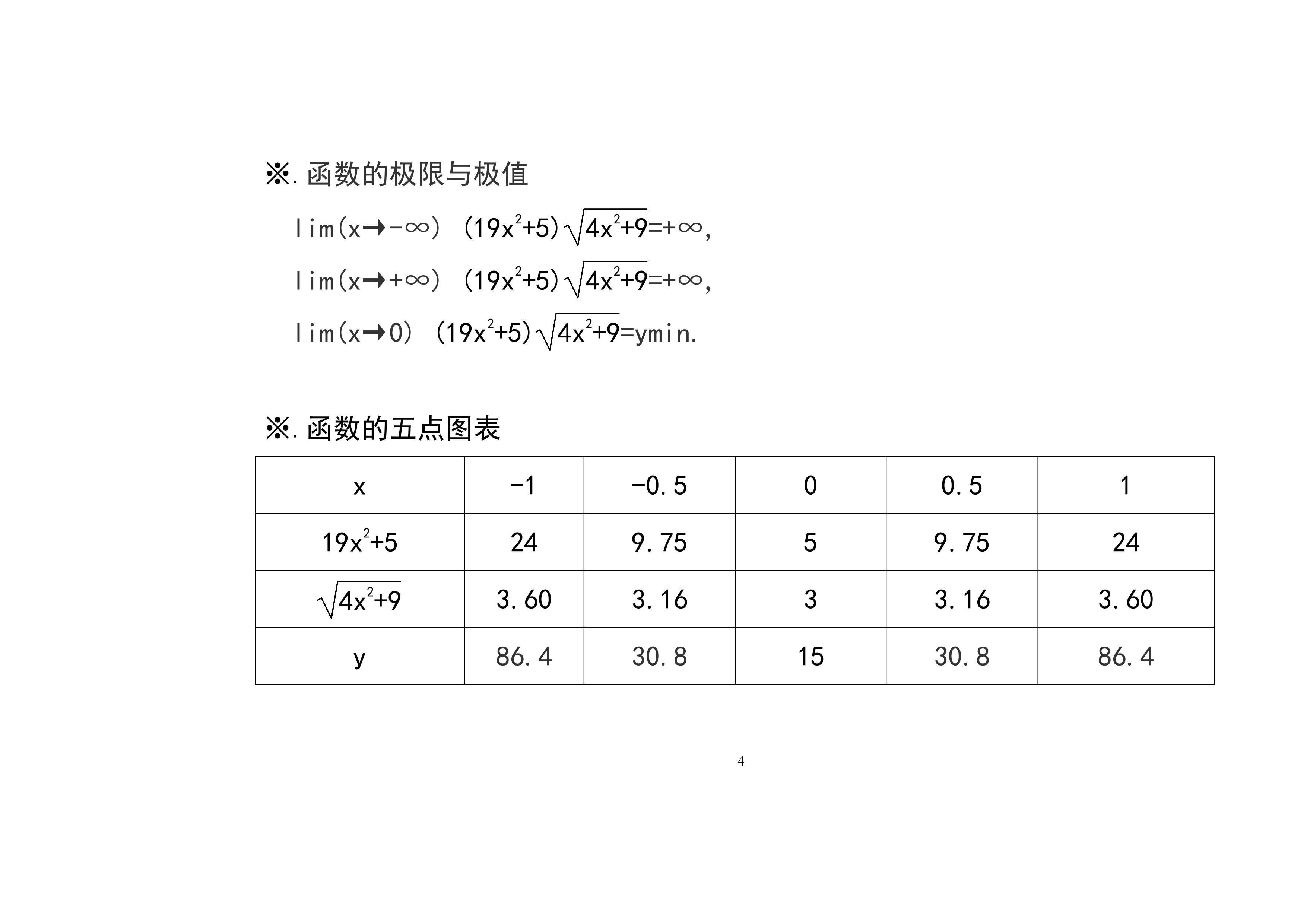
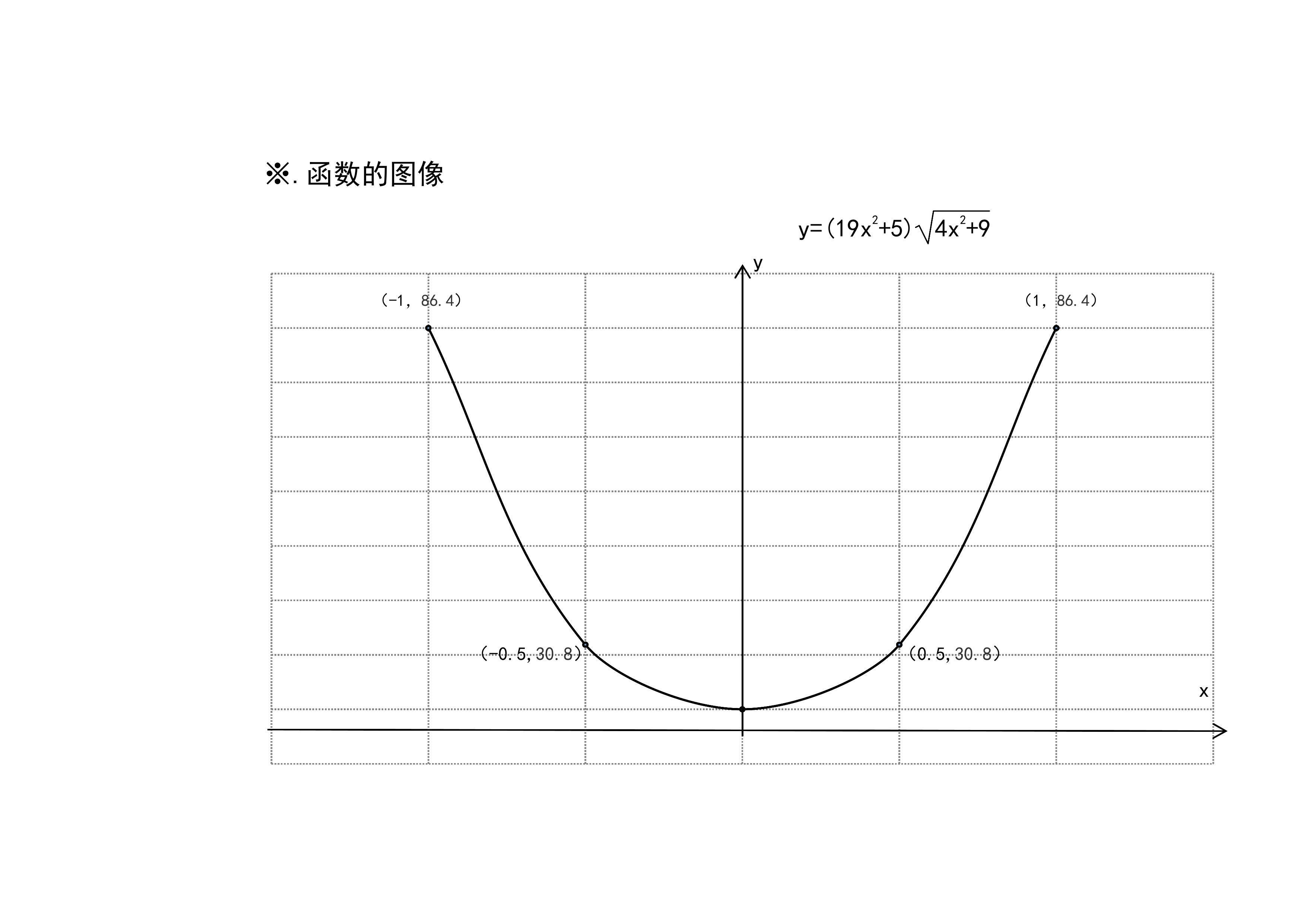
2.函数y=(19x2+5)√(4x2+9)的主要性质及其图像:介绍函数的定义域、单调性、凸凹性、极限等性质,列举函数的五点图表,进一步画出函数的示意图。
\n\n
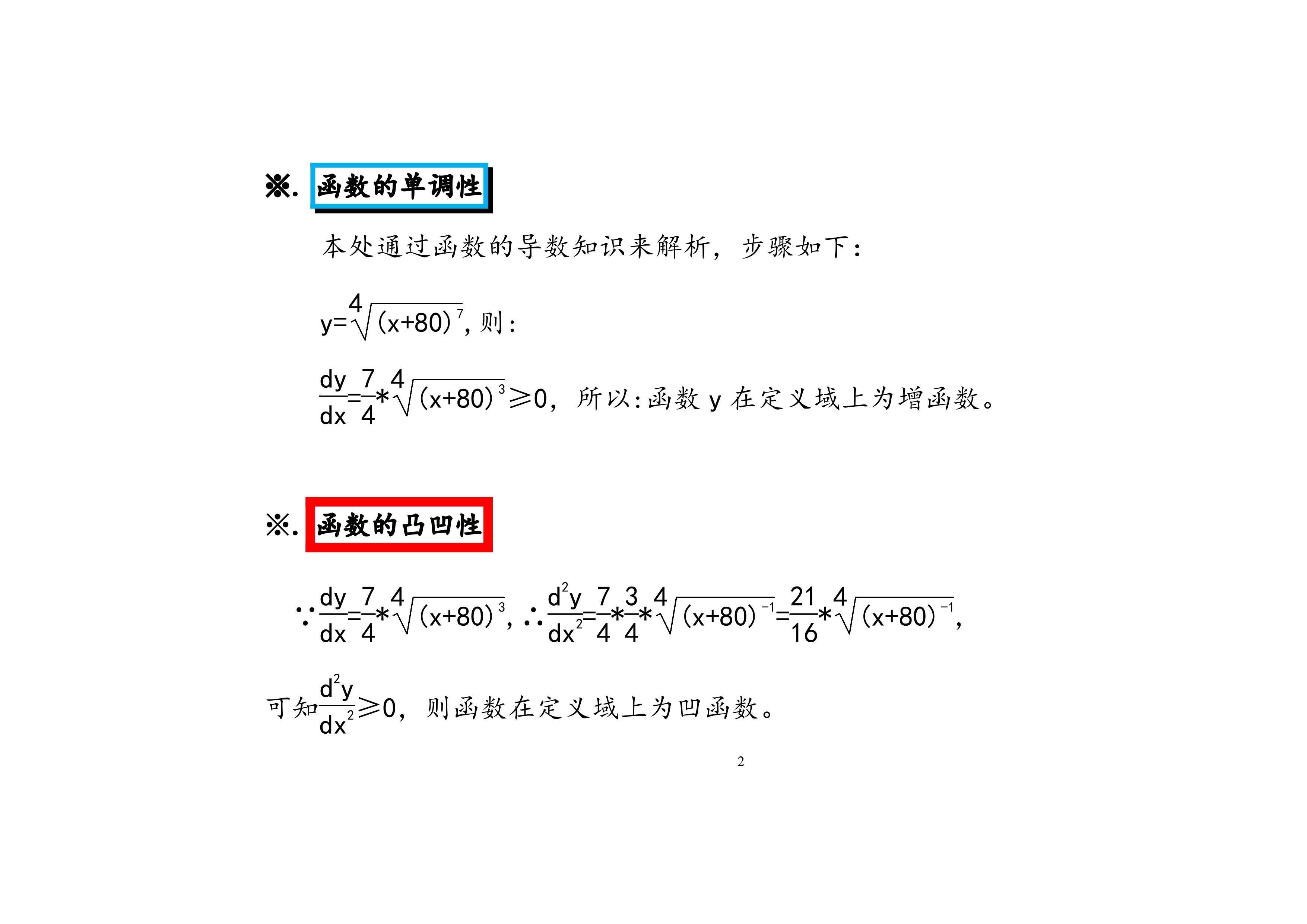
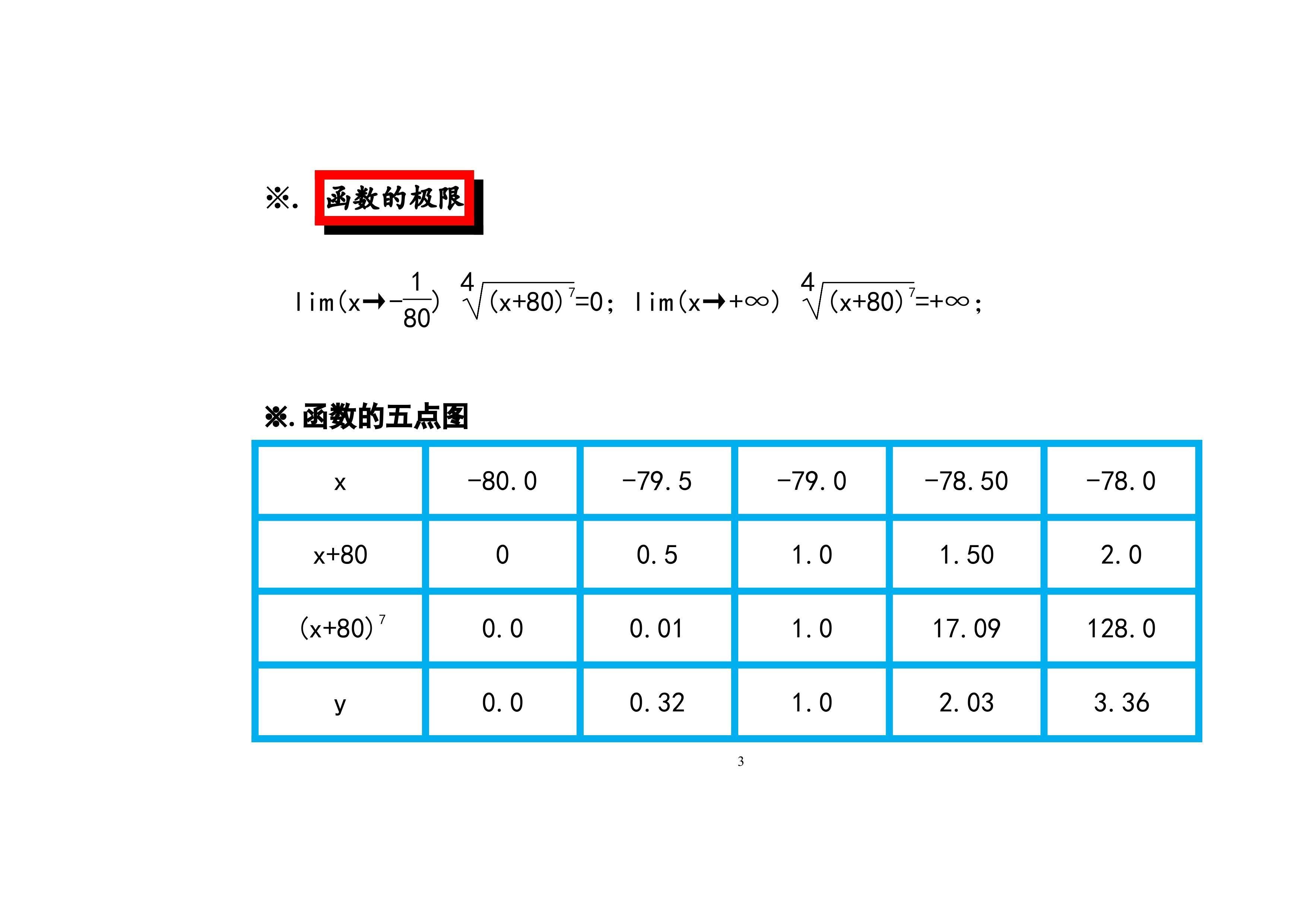
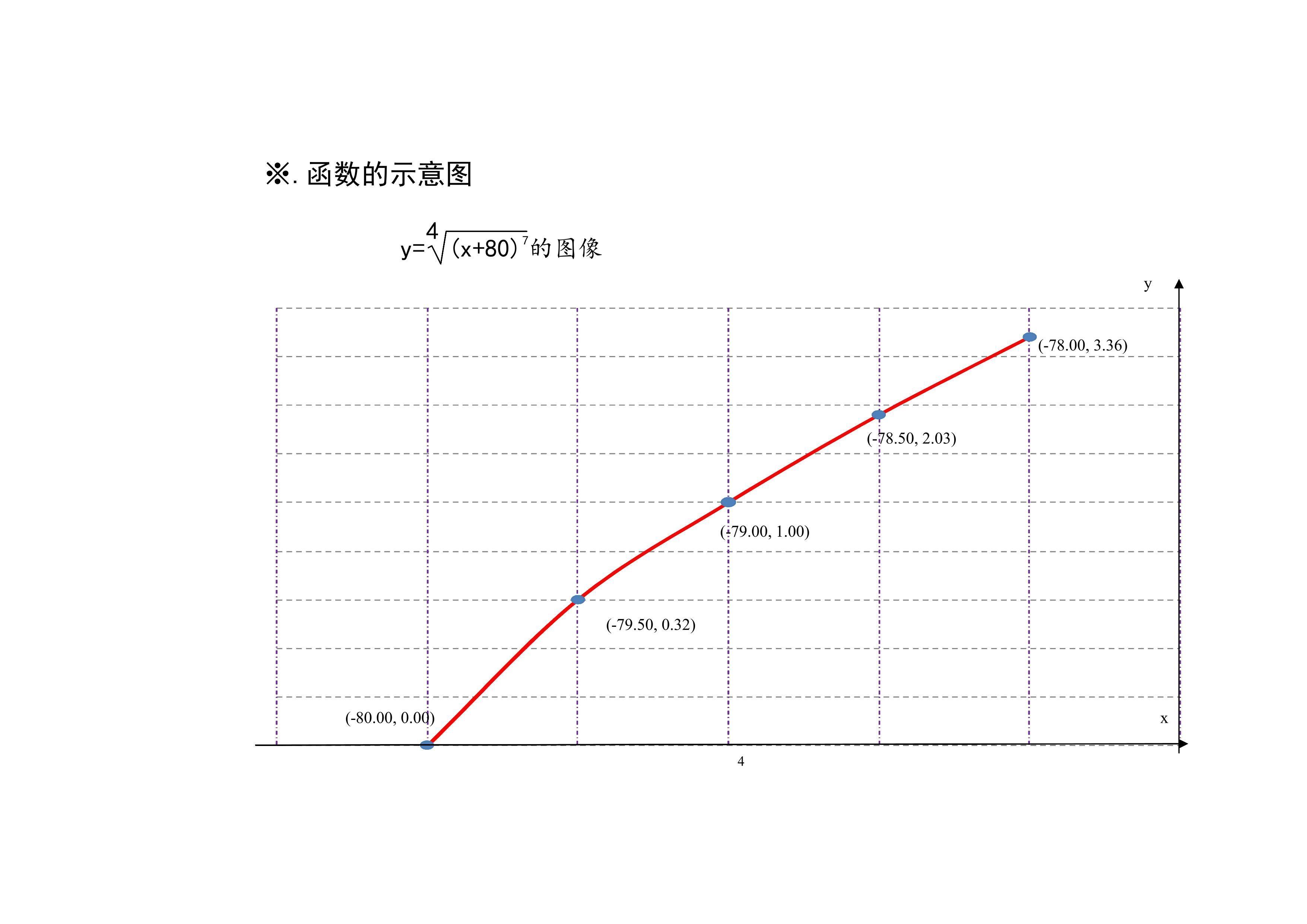
3.函数y=4√(x+80)^7图像画法及步骤:本文通过函数的定义、单调、凸凹性和极限等性质,介绍函数的主要性质及图像画法步骤。
\n\n
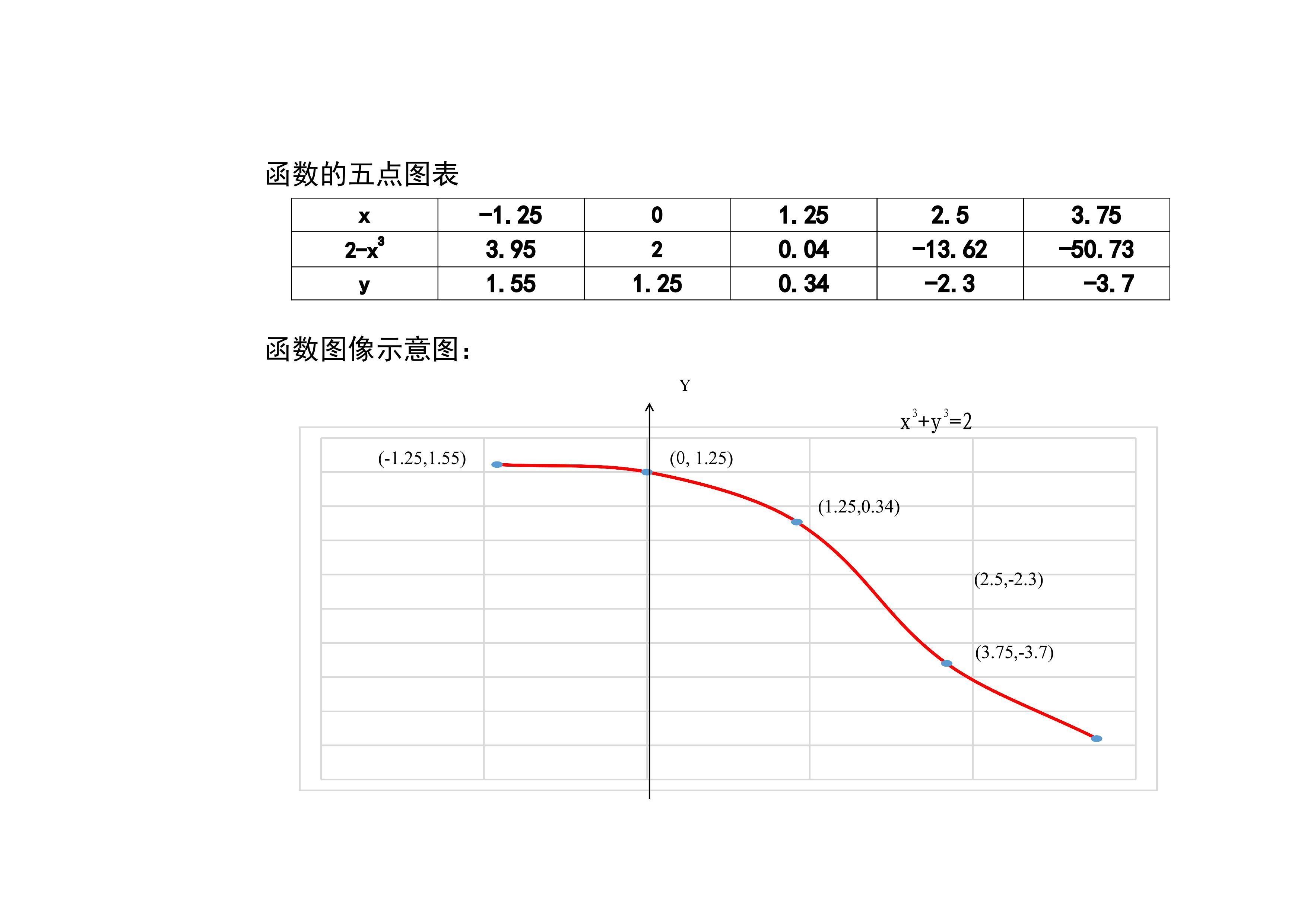
4.曲线x³+y³=2的主要性质及其图像示意图:介绍曲线方程的定义域、单调性、凸凹性等性质,同时用导数的知识求解函数的单调区间和凸凹区间,并简洁画出函数的图像示意图。
\n\n
5.√(x+4)+√(3y+5)=2的图像示意图:介绍曲线方程的定义域、单调性、凸凹性及极限等性质,同时用导数简洁画出函数的图像示意图。
\n\n
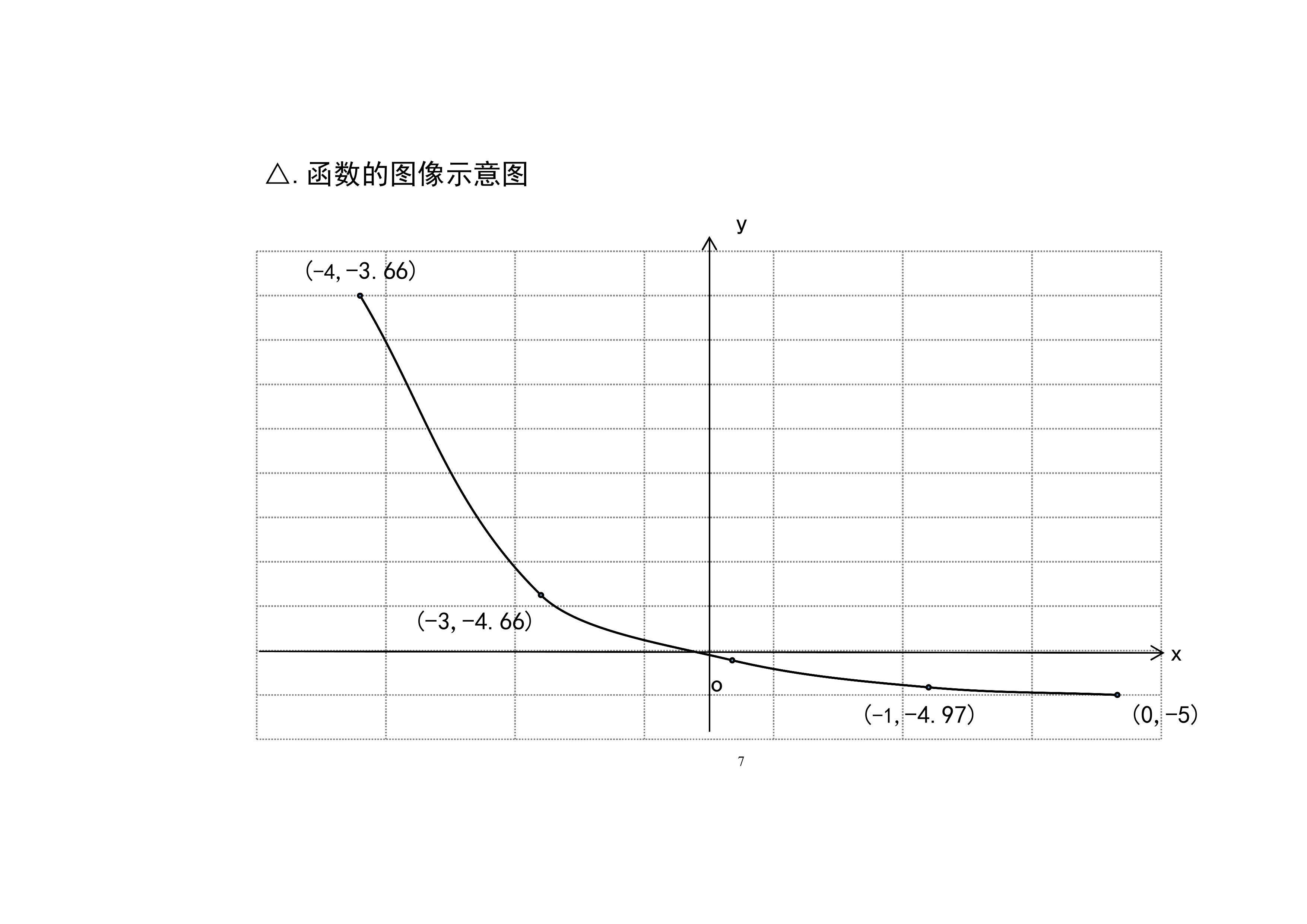
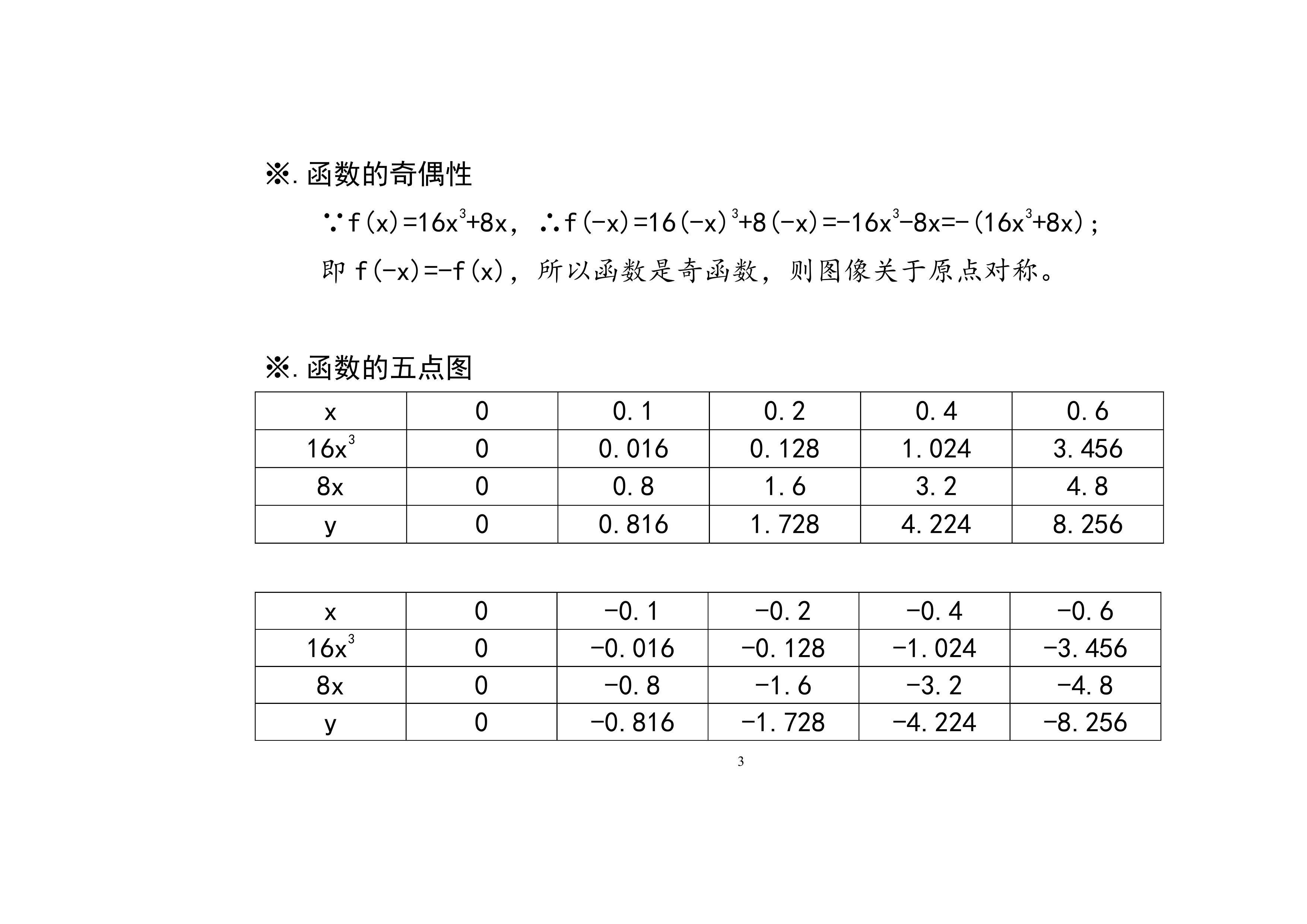
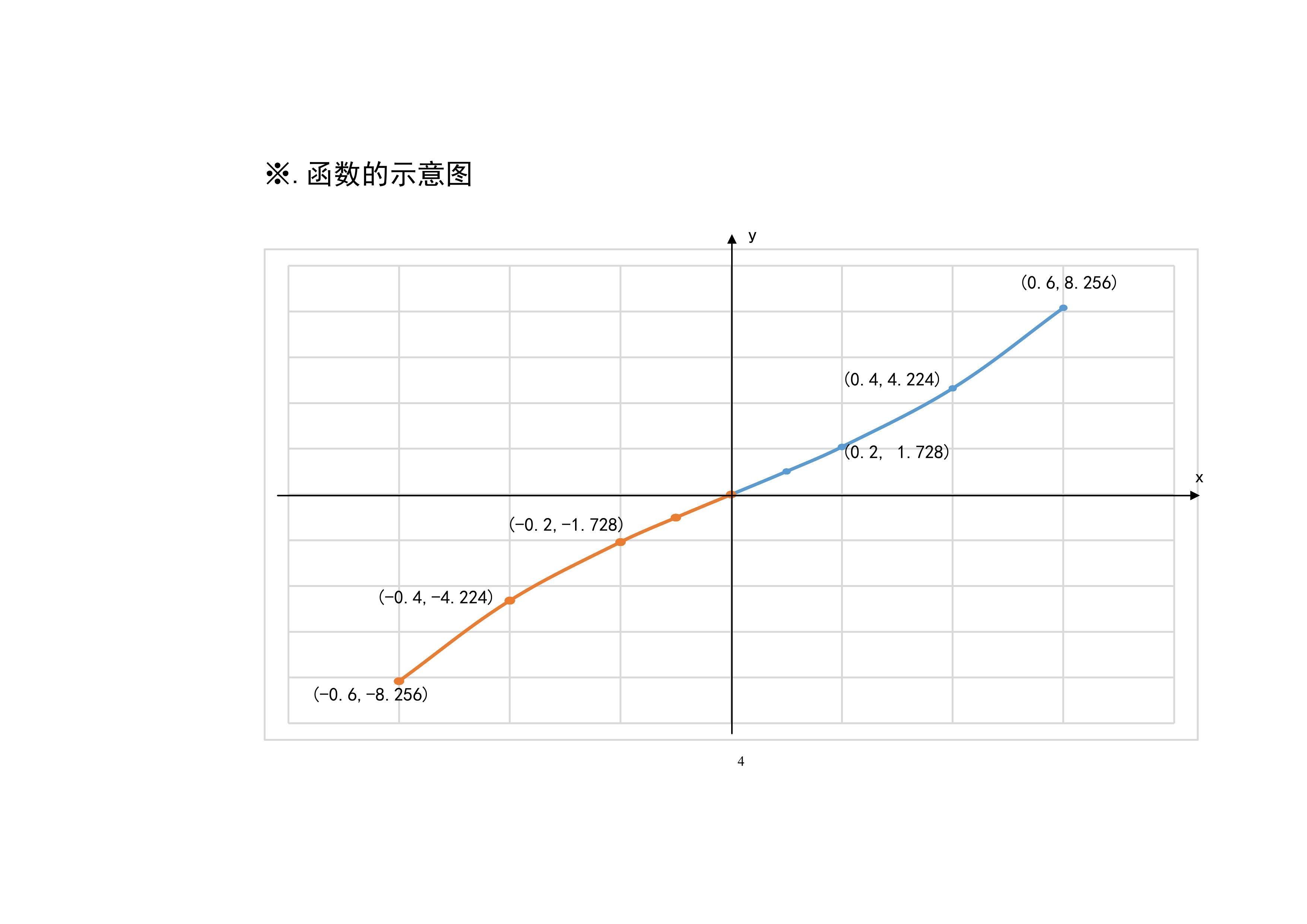
6.函数y=16x3+8x的图像示意图及主要性质:介绍函数的定义域、单调性、凸凹性、极限等性质,列举函数的五点图表,进一步画出函数的示意图。
\n\n
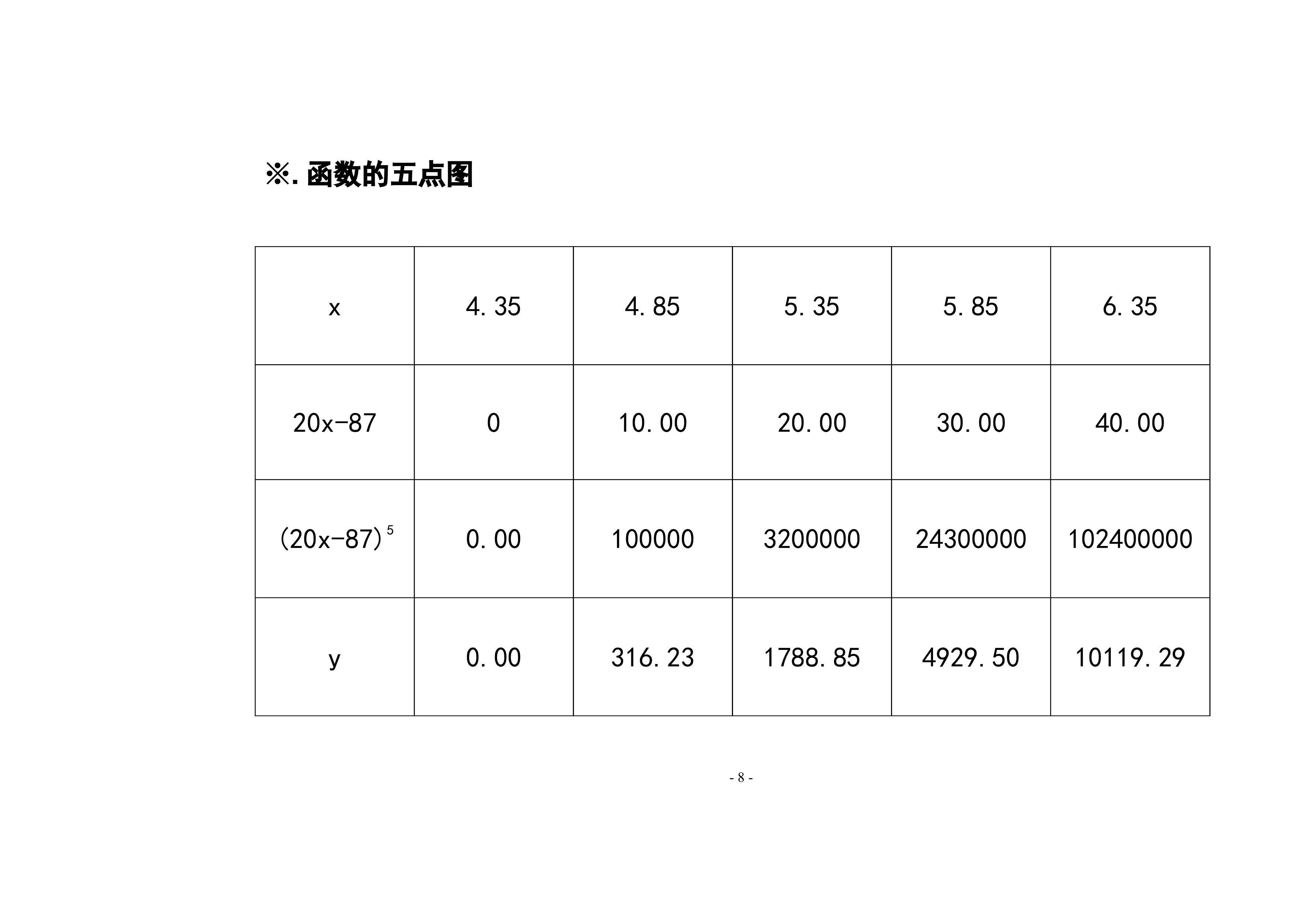
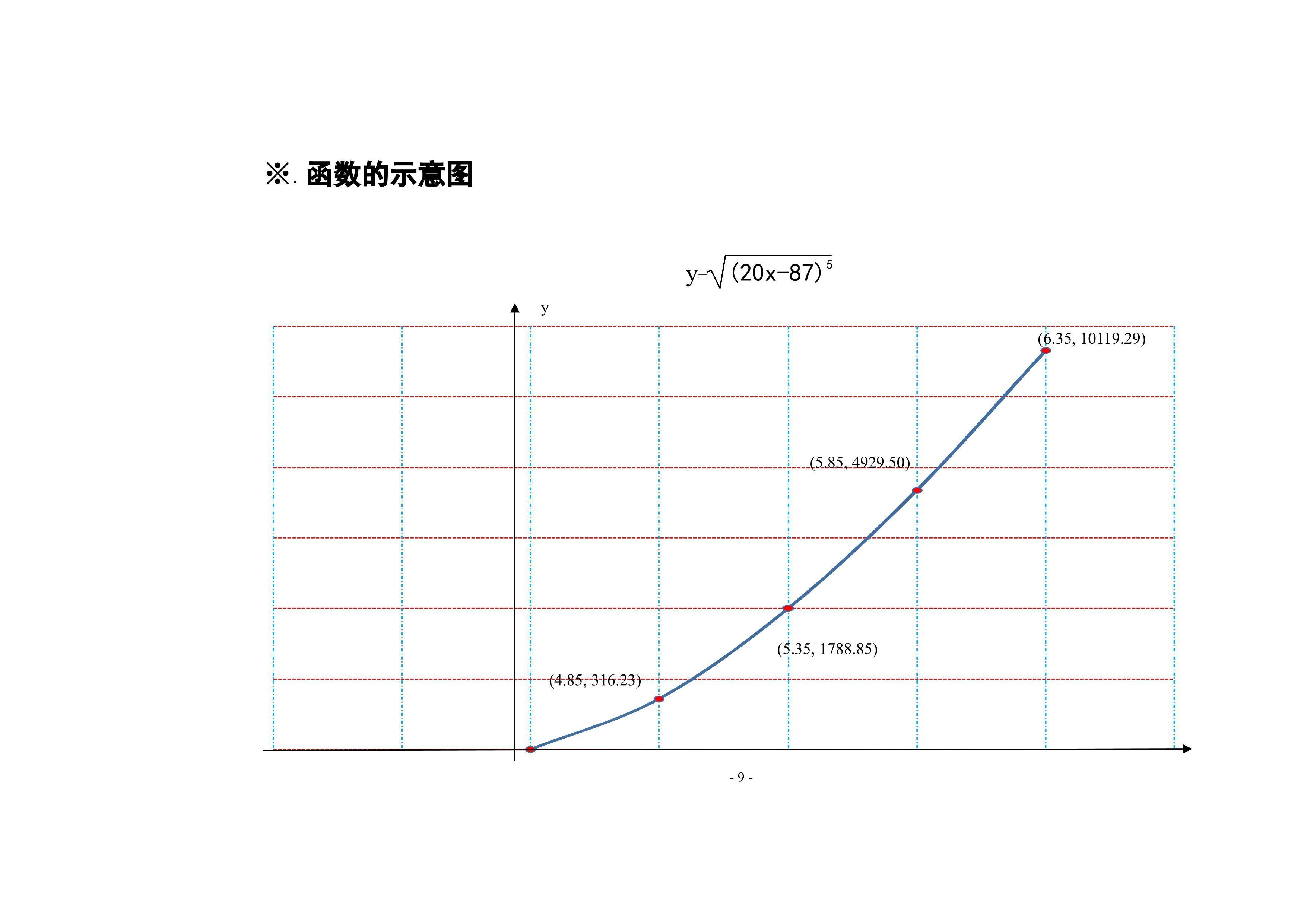
7.函数y=√(20x-87)^5图像画法及步骤:通过函数的定义、单调、凸凹和极限等性质, 并通过导数知识,介绍函数的主要性质及图像示意图画法步骤。
\n\n
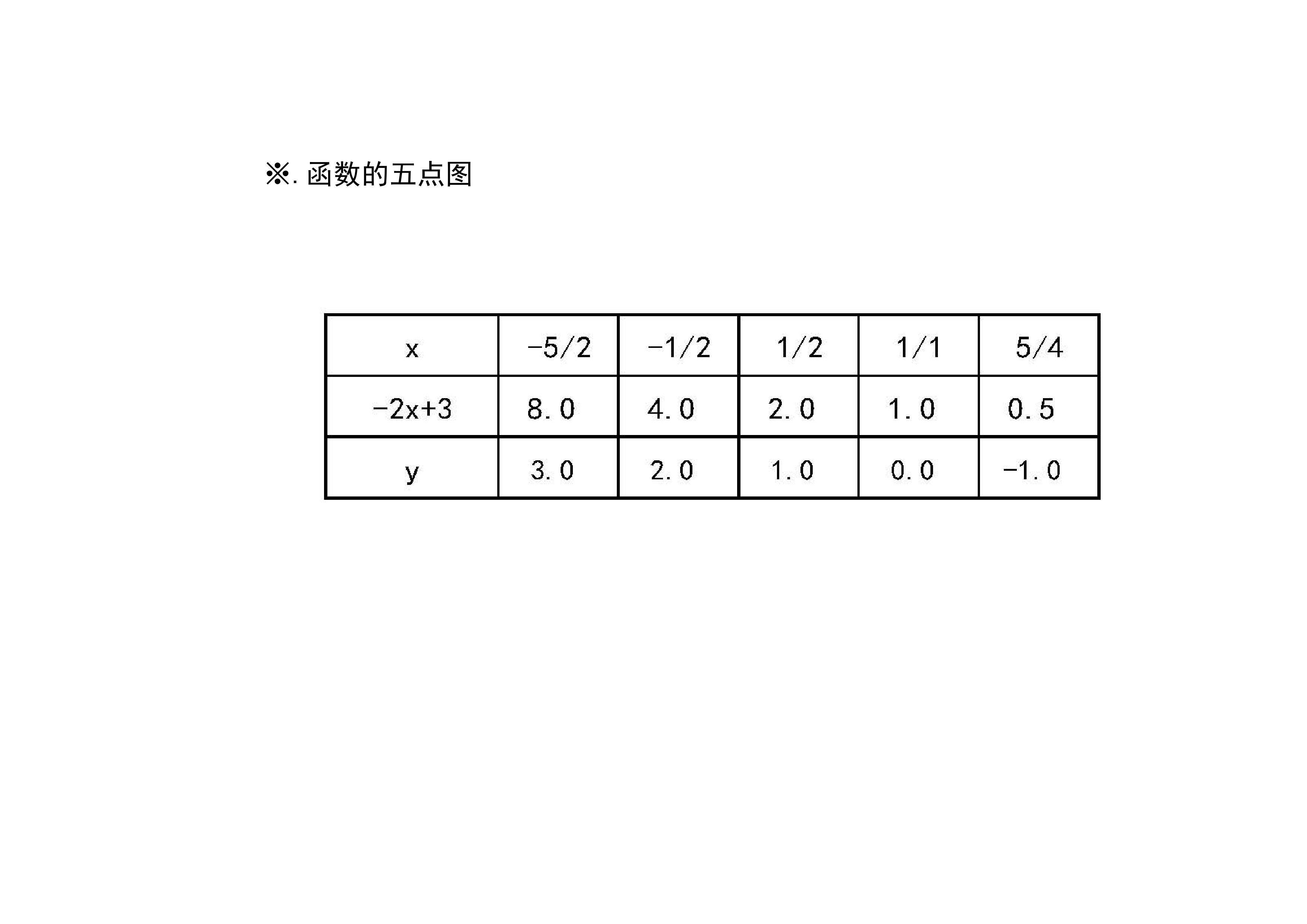
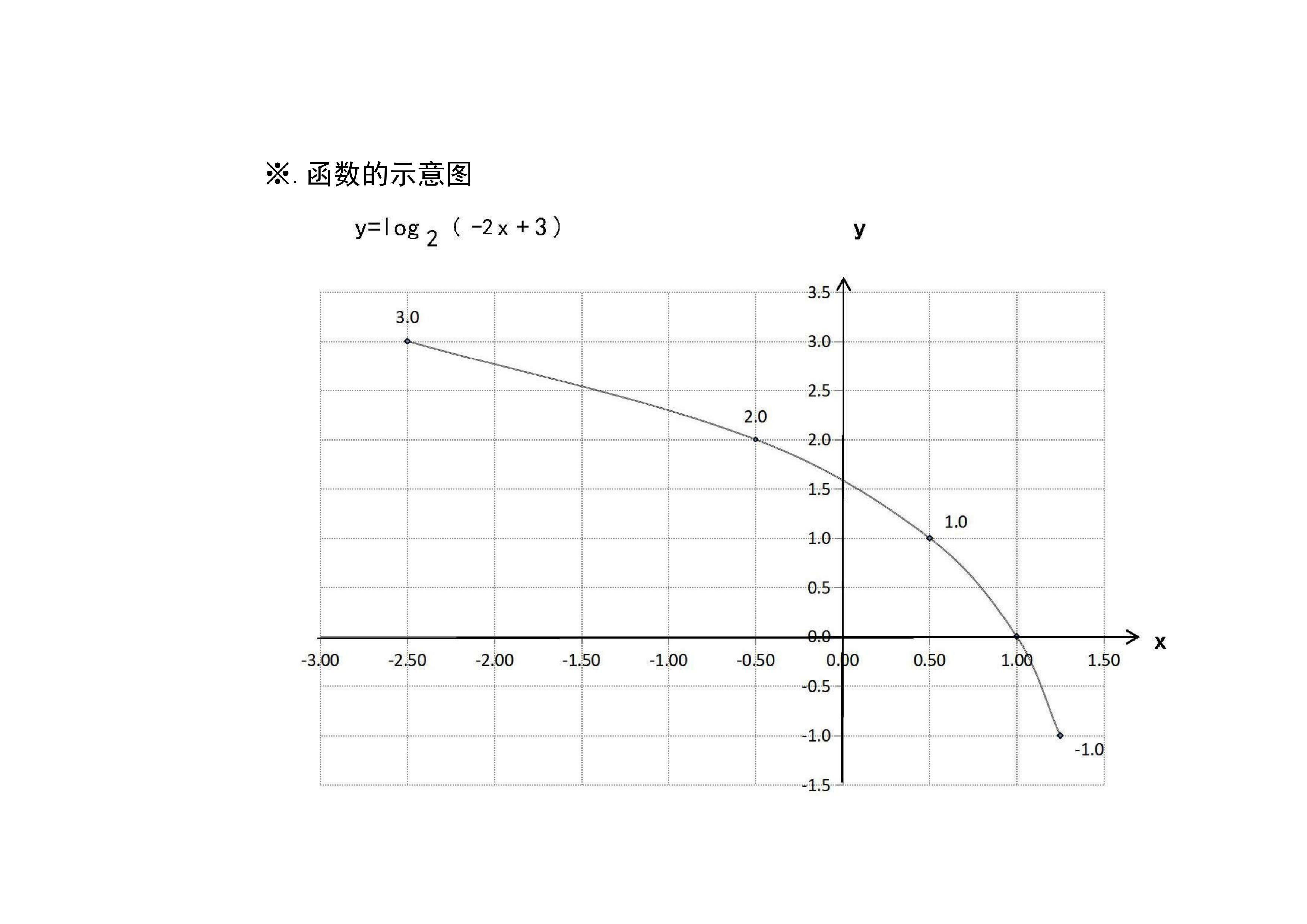
8.函数y=log2(-2x+3)的图像示意图:介绍函数的定义域、单调性、凸凹性、极限等性质,列举函数的五点图表,简要画出函数的示意图。
\n\n
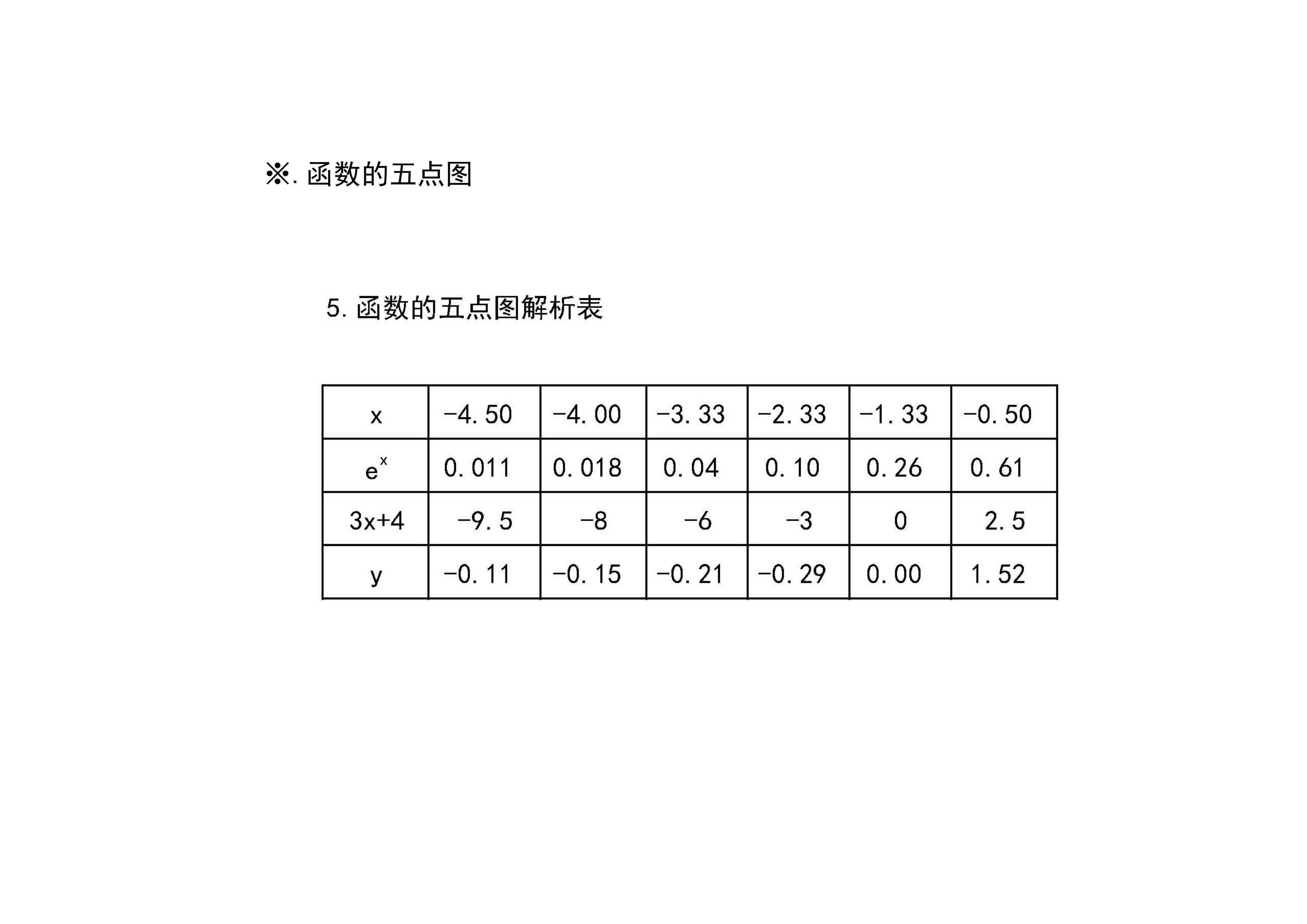
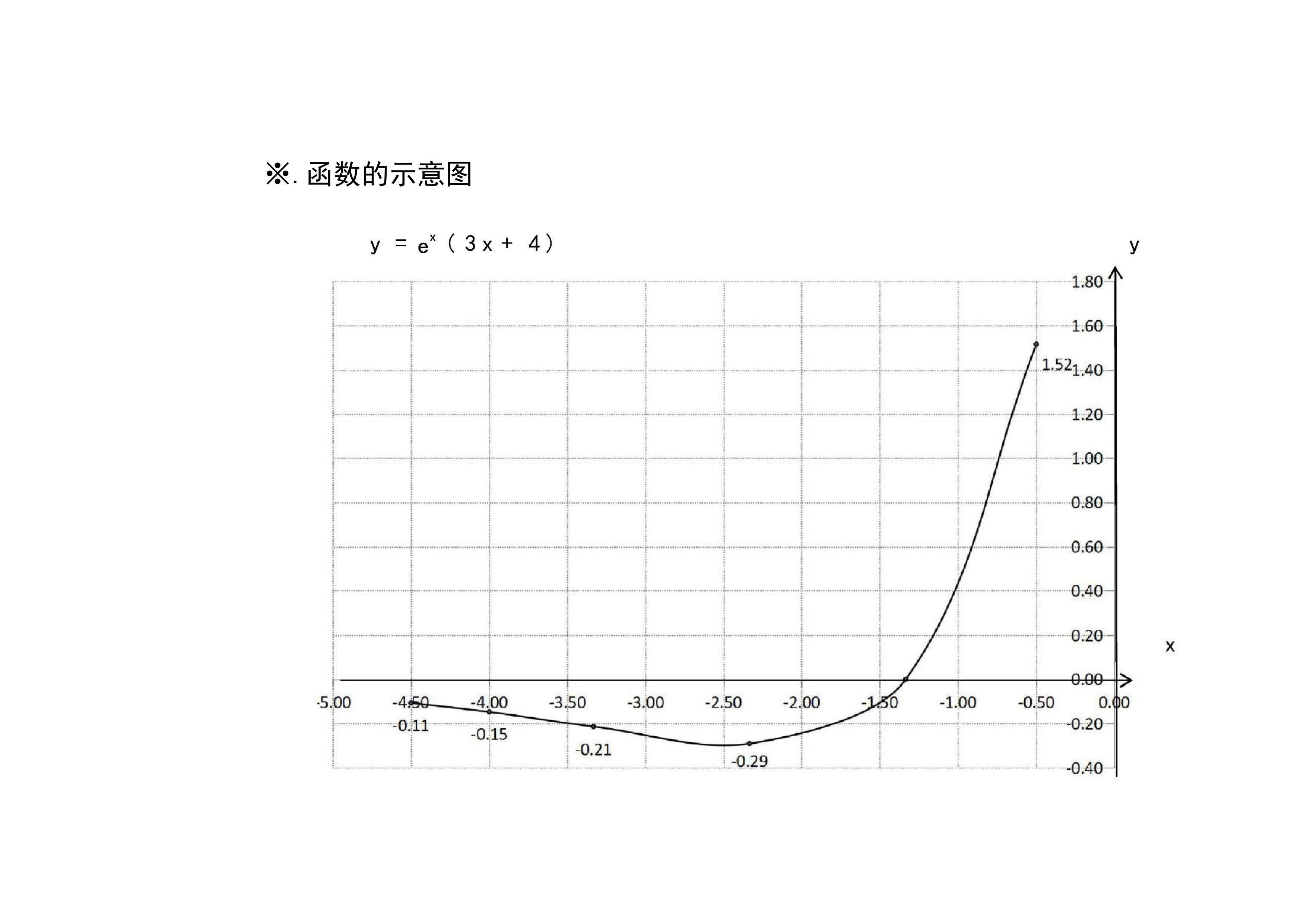
9.函数y=e^x(3x+4)的图像示意图:本文通过函数的定义、单调、凸凹性和极限等性质,介绍函数的主要性质及图像画法步骤。
\n\n
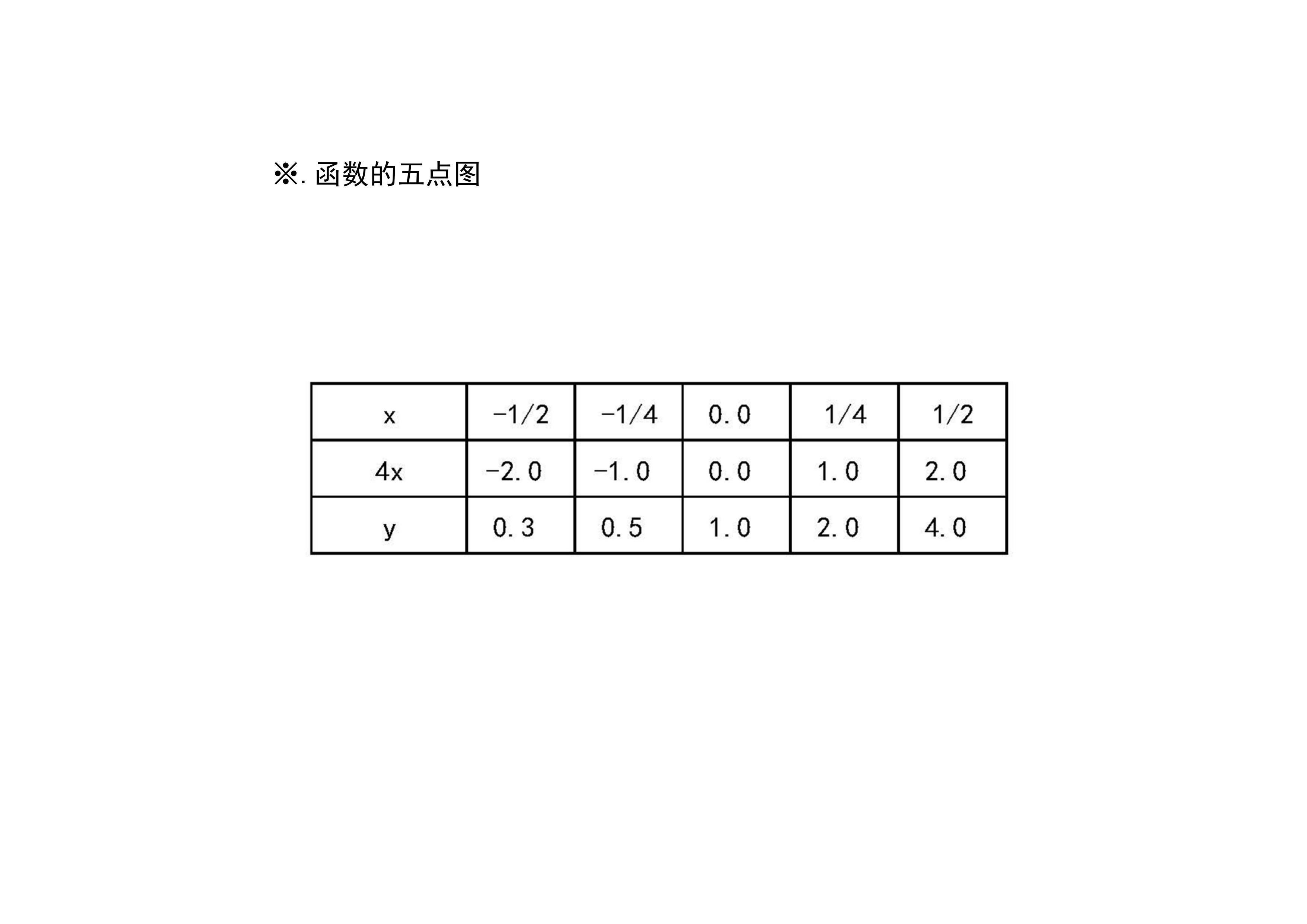
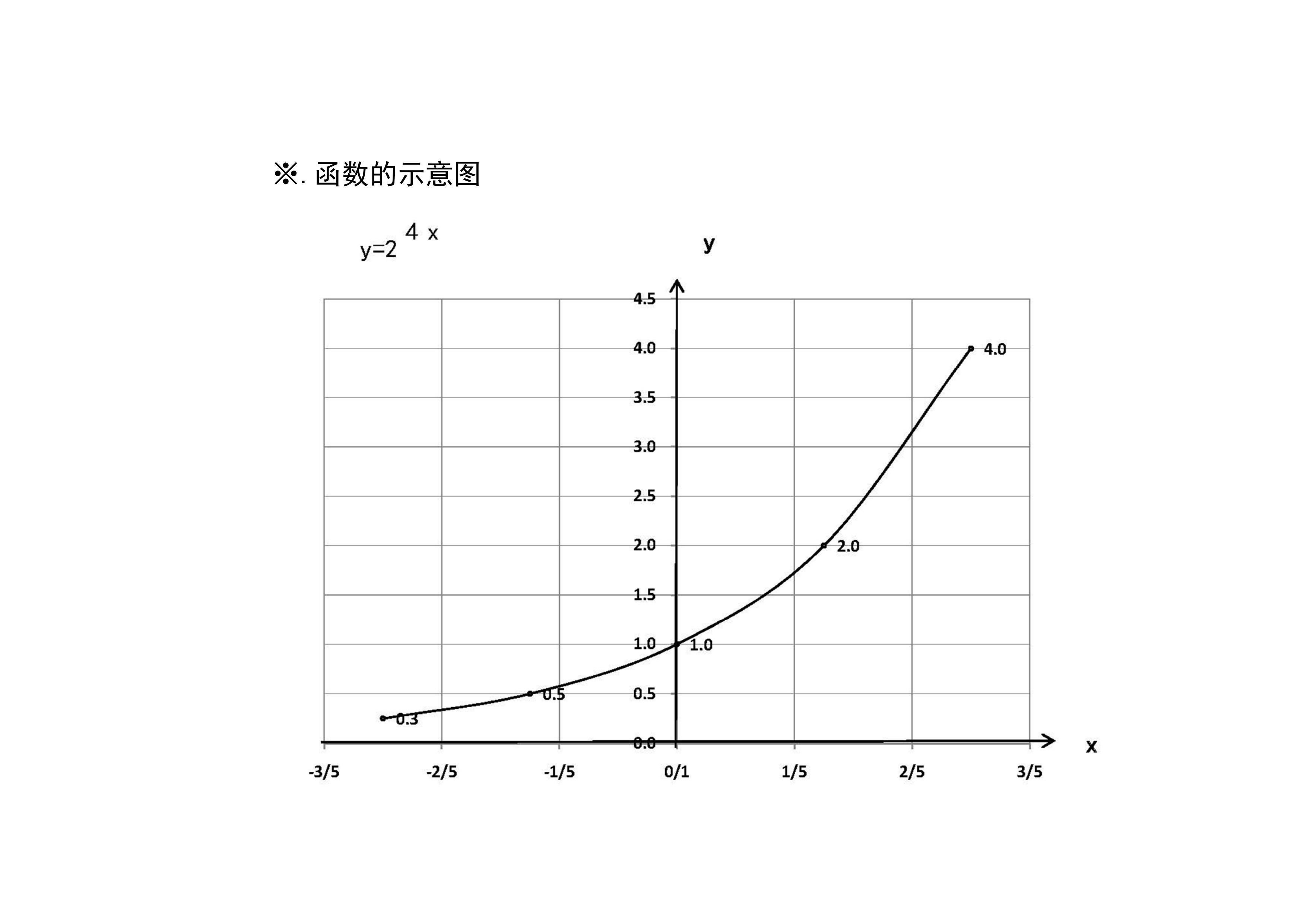
10.函数y=2^4x的图像示意图:介绍函数的定义域、单调性、凸凹性、极限等性质,列举函数的五点图表,进一步画出函数的示意图。
\n\n
\n\n
































","gnid":"9758824ec7671aa4d","img_data":[{"flag":2,"img":[{"desc":"","height":925,"title":"","url":"https://p0.ssl.img.360kuai.com/t01a370aba0dc0184ae.jpg","width":1280},{"desc":"","height":925,"title":"","url":"https://p0.ssl.img.360kuai.com/t01fe729509bf6963a8.jpg","width":1280},{"desc":"","height":925,"title":"","url":"https://p0.ssl.img.360kuai.com/t01c644eeab94a0efe6.jpg","width":1280},{"desc":"","height":925,"title":"","url":"https://p0.ssl.img.360kuai.com/t013539215e0a83c2a4.jpg","width":1280},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t011ac510957e2c014e.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01b6300bde0321b12c.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t010ec62f9edc968eba.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t012ea8cadd7067c59a.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0135e6b9e5ad5f2723.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0101a95b931e2c6661.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0156869fd05f1b9bb9.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01eeb16f6ae9877b62.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01fd234f62dc83b806.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01a7177f0c14cf1b67.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01f3e9bcbfa66207be.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0111341fafd83e8b23.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01b12ae4529c0fc1a5.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01c2d414e70ce33022.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01a6435466e13d89c7.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0179a153481db89522.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t013f7979ab67311565.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t012871721b42a710c1.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t013b8fb94c7da143c9.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t015c6380a9e4dd5da4.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01c8edbb39b9d7fe87.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0122b1ab788e519a35.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01b446dfdddb35e4bf.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01651411583c303362.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0126094f1ca9ed1956.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t018fabf5214cdfc785.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t015b3f1e97b4dbe1ae.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01190830f3a32242fd.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01f1055028c526dd9d.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01e3ef63beab75c785.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t011dde9de6ce8a849b.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t019e8dbf2156e3031f.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t017d660aed63d492fa.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t017d660aed63d492fa.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0173f2a15f98505230.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0121e883d03506ad7f.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01fd20ffaf7942432d.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0174518a47ce9dd664.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t013e8e7b19fa695693.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0130fe2d9574be5db9.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0143c4b32aae3b438c.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01f74b752f697884fa.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0117c554a911c21419.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0141cfbe536892d640.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01d396d571728906e5.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01c87a38b737bd03fb.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t018eaaf25c81dbece5.jpg","width":"3509"}]}],"original":0,"pat":"pdc,art_src_0,fts0,sts0","powerby":"pika","pub_time":1711495200000,"pure":"","rawurl":"http://zm.news.so.com/7339c860ffebb01ebf215d79eb02f630","redirect":0,"rptid":"65e62da3ddba0208","rss_ext":[],"s":"t","src":"仁新数学","tag":[],"title":"导数五步法画函数图像10个函数示意图应用举例之一
邱空有3771y=xe^x+1的导数为什么会是y'=e^x+xe^x,还有y=xe^ - x的导数是怎么求的呢. -
秋泡功13456881176 ______[答案] y'=(xe^x)'+(1)=(x)'*e^x+x*(e^x)'+0=e^x+xe^x xe^x 这个不是 两个函数 搞一起了吗 套公式 Ok 了 打错了吧?y=xe^-x 这个是什么? 如果是这个的话 ← y'=xe^x-x=e^x+xe^x-1 很简单的啊
邱空有3771紧急!(1+a/x)e^x求导(1+a/x)e^x怎么求导? -
秋泡功13456881176 ______[答案] 导数=(1+a/x)'*e^x+(1+a/x)*(e^x)' =(0-a/x²)e^x+(1+a/x)*e^x =(1+a/x-a/x²)e^x
邱空有3771求xy=e的(x+y)次方的导数.要详解. -
秋泡功13456881176 ______[答案] xy=e^(x+y) 所以两边对x求导数得到 y+xy'=e^(x+y) * (1+y') 所以y'=[e^(x+y)-y]/[x-e^(x+y)]
邱空有3771(e^x+1)^( - 1)求导 -
秋泡功13456881176 ______[答案] -(e^x)/[(e^x+1)^2]
邱空有3771e的x次方分之一 的导数 我算的是负的e的x次方分之一请看好了!是(e的x次方)分之一 的导数,不是e的(x分之一)次方 -
秋泡功13456881176 ______[答案] 对 我算的也是这个 这是复合函数求导问题 对外层函数求导结果是 —1/e^2x 对内层求导结果是e^x 二者相乘结果就是楼主的答案
邱空有3771y=(e^x+e^ - x)/2的导数怎么求急啊! -
秋泡功13456881176 ______[答案] e^x的导数是他自己,即e^x,e^-x的导数为-e^-x,所以=(e^x+e^-x)/2的导数y'==(e^x-e^-x)/2
邱空有3771导数f(x)=x(e^x - 1) - 1/2 x^2求出的导数是f'(x)=e^x - 1+xe^x - x=(e^x - 1)(x+1)还有,带e的导数是怎么回事? -
秋泡功13456881176 ______[答案] f(x)=x(e^x -1)-1/2 x^2=xe^x -x-1/2 x^2 f'(x)=x'e^x-x(e^x)'-1-x=e^x-xe^x-1-x xe^x是一个复合函数求导,根据(AB)'=A'B+AB'公式求就可以了,e^x的导数就是它本身,1/2 x^2和x求导利用(x^n)'=nx^(n-1)求.
邱空有3771数学 - e^ - x+1 的导数是什么,怎么算 -
秋泡功13456881176 ______ y=-e^(-x+1), 利用复合函数的链式求导法则:y'=-e^(-x+1)*(-x+1)'=e^(-x+1)
邱空有3771用导数证明e的x次幂大于1加x,x不等于零. -
秋泡功13456881176 ______[答案] 要证明e^x>1+x 也就是要证明e^x-1-x>0 然后对e^x-1-x求导就是e^x-1 然后当x>0的时候e^x-1是恒大于0的,那么e^x-1-x是递增的,当x=0时,e^x-1-x=0,所以在x>0的时候e^x-1-x>0恒成立 同时当x0对于不同的x都是恒成立的 所以e^x>1+x
邱空有37714/ex+1的导数,就是4除以e的x次方加1的导数,请写明过程, -
秋泡功13456881176 ______[答案] 上式=4乘以e的负X方加1.e的负X方加1的导数为负的e的负X方.故上式答案为负4的e的负x方


















































