自学数学怎样学得最快

困扰学界几十年的集合难题，竟被圈外人一个月搞定？？？

是的，你没看错。

当事人Justin Gilmer，毕业已7年，目前是谷歌研究员，于数学界并无名头，连其导师也并不看好他所做的研究，以至于成果发表后——

牛津、普林斯顿等高等学研机构数学家们看到名字，纷纷好奇：

这人谁啊？

不仅身份引人好奇，其破题方法也不按圈内常规路数，个中灵感来自通信祖师爷香农的信息论。

这项开创性成果及幕后历程刚被一些媒体介绍，在Reddit和Hacker News上引来不少网友热议。

有网友表示：看到信息论在意想不到的领域应用，真是酷炸了。

还有网友就着话题，秀了一把自己以信息论解决问题的经历。

所以，这位远离纯数学学术研究的大哥解决了什么问题？又如何在一个月内搞定的？

往下看。

这个猜想究竟是什么？

这位谷歌研究员突破的难题，名叫union-closed sets conjecture（并封闭集合猜想）。

该猜想认为，对于一个包含至少2个集合的、对并运算封闭的有限集合族，至少存在一个元素，使得它在至少一半的集合里出现过。

我们来解读一下这个猜想说的啥。

首先集合，就是包含了一系列元素的合集，这里面的元素既可以是数字，也可以是变量等。

例如这是一个我们常见的数集，而且是有限的（只包括3个元素）：

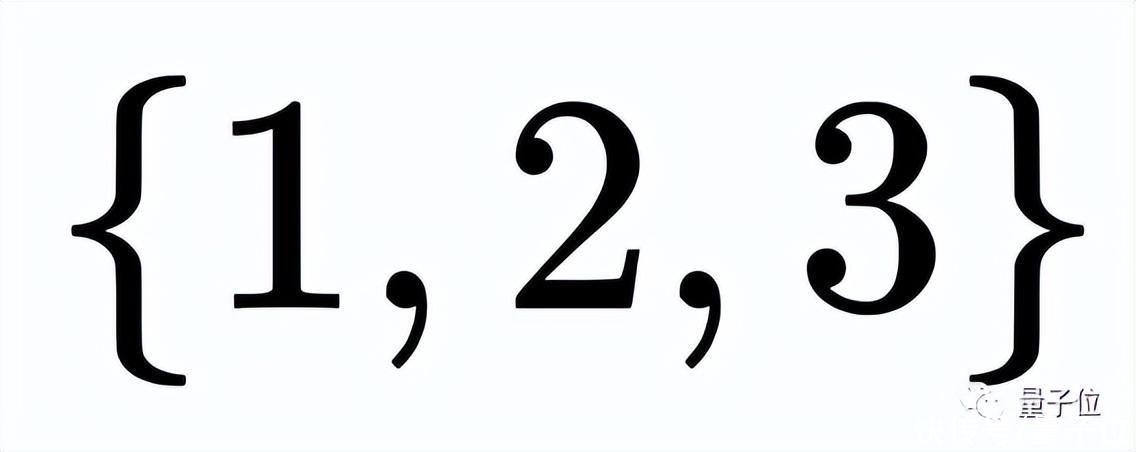
（至于无限数集，就像是自然数集、有理数集、整数集这种由无限个元素组成的集合）

当然，集合也有集合，它们组合起来，就可以被叫做集族，例如下图中F就是一个集族：

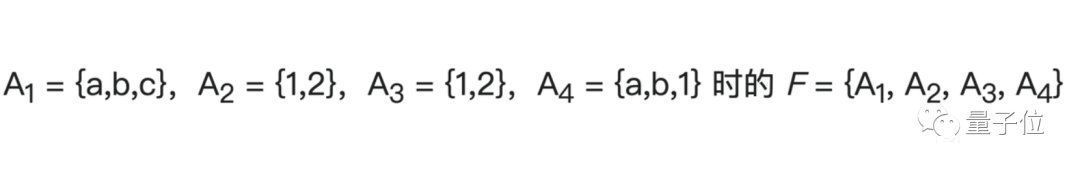
在这些集族中，有一类特殊的集族对并运算封闭。

对集族中的集合而言，并运算就是对两个集合求并集；至于并运算封闭，即是指在对任意两个集合进行并运算后，其结果仍然在这个集族中。

以下面这个集族为例：

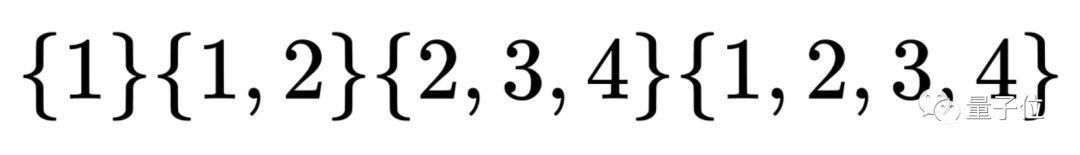
无论是对{1}、{1,2}求并集，还是对{2,3,4}、{1}求并集，还是对{1,2}、{2,3,4}求并集……任意两个集合求并集，其结果都会在这个集族中。

所以，上面这个集族就符合并封闭集合这一要求，而并封闭猜想也正是基于此而提出。

值得注意的是，这一猜想中的“一半”是紧致的，毕竟对于任何一个集合的子集族，所有的元素恰好在一半的集合里出现过。

它于1979年被一个叫Péter Frankl的数学家提出，所以也一度被叫做Frankl猜想。

看起来似乎不难，然而到实际解决时，一众数学家才发现这并不简单。

△Peter Winkler

达特茅斯学院数学教授Peter Winkler曾经在1987年就这个猜想给出尖锐的评价：

△对此有同行表示，起源至少没答案难orz

为了解决这个问题，数学家们也已经尝试过不少方法。

例如有人试着给猜想加上一些限制条件，让它在这些情况下成立。

像是将它和图论中的二分图（Bipartite Graph）联系起来，证明具备其中某种性质的集族，在这个猜想的条件下成立。

又或是给其中的元素加以限制，再加以证明……

BUT，无论是哪种方法，距离真正需要证明的猜想都还差不少距离。

来自哥伦比亚大学的助理教授Will Sawin对此评价称：

问题就这样进度缓慢，直到2022年秋天，谷歌研究员Justin Gilmer借着朋友结婚的契机，回到了罗格斯大学校园。

用信息论突破了1%

Gilmer回母校的时间是2022年10月，此时距他毕业离开数学学术圈，已过去7年。这些年来，他自觉无心专注纯数学领域，转而自学编程，投身了IT行业。

此次返校，他拜访了导师萨克斯，还四处转了转。

就在散步中，他突然回忆起——当年自己徘徊于校园小径，苦苦思索的一个数学问题：

没错，就是那个对“并封闭集合猜想”的证明。

读博期间，Gilmer绞尽脑汁，花了一整年时间却毫无进展，只是搞明白了为什么这一看似简单的问题难以解决。

为此，他还去找过导师萨克斯。但导师也曾在该问题上停滞不前，因而他既不看好Gilmer的研究，也不愿重新碰这一领域。据Gilmer回忆，当时导师差点把他赶出房间。

但现在，重回校园转一圈的Gilmer有了个新想法：用信息论及相关原理解决并封闭猜想问题。

△ 信息论奠基人 克劳德・香农

信息论发源于20世纪上半叶，其最为出名的论文是香农在1948年发表的《通信的数学原理》，其中提出以“消除不确定性”的多少，来评价通信过程中的信息量大小。

这个不确定性要怎么理解呢？

以掷硬币游戏为例，假设我们需要掷5次硬币，然后输出结果序列，每次结果为1比特。

如果现在我们抛掷的是一枚普通硬币（正反概率各50%），那么我们至少需要5个比特来传递信息。

但如果给这枚硬币做点手脚（让它正面朝上的概率99%），我们就完全可以提前规定，在硬币5次都是正面朝上时，只用1个比特来传递信息。

这样，被用以衡量文本、图片等内容大小的比特，也能成为描述事件发生不确定性的信息熵单位，而信息论也成为现代通信奠基之作，构建起今日的信息社会。

受到信息论的启发，Gilmer决心下场再战。

此后一个月中，他利用下班后的晚上及周末时间，试探性地进行了摸索。有意思的是，由于长时间未接触理论，他一边研究还一边拿着本信息论教科书，以备随时查阅。

研究过程中，Gilmer还发现自己研究的问题并非无人关心，其实几年前，就有几位数学家在菲尔兹奖得主Tim Gowers博客里探讨过该问题。这让他有了更多信心。

△ Tim Gowers博客的相关研究内容

Gilmer的思路是找反例。

根据并封闭集合猜想，一个正常的并封闭集族中，至少应该有一个元素在多于一半的集合中出现。

既然如此，只要想办法构造一个特殊的集族，里面没有一个元素出现在超过1%的集合中，这个猜想就会被证伪，反之如果构造不出来，那么猜想就可能成立。

现在，我们用信息论视角看这一猜想：

正常来说，如果从集族中任意挑出两个集合，这两个集合取并集后，并集中的元素比原来两个集合更多，其信息熵应该比原来的单独两个集合更低。

然而如果基于“没有一个元素出现在超过1%集合”这个限制条件，任意两个集合取并集后，计算出来的信息熵竟然比原来的单独两个集合更高。

这显然是不可能的，因此不存在这么一个特殊的集族，Glimer的反例也没有找到。

但这也就意味着在“并封闭”集族中，至少存在一个元素，会出现在超过1%的集合中。

2022年11月16日，Gilmer将这一思路写成论文，发表在了arXiv上。

当然，他这篇论文还不是“完全体”，也就是说并没有完全证明并封闭集合猜想——

毕竟这只是至少1%，还不意味着原来的并封闭集合猜想中的至少50%就成立。

但这个新思路已经足够让学界震动。

普林斯顿大学数学家Ryan Alweiss评价“引入信息量”这一操作：非常聪明。

仅仅几天后，就有3个不同的数学研究组基于他的研究，先后发表了研究论文，随后也有更多研究者跟进，他们所在院校机构有牛津、普林斯顿、哥大、布里斯托等。

在后续研究中，对“并封闭集合猜想”的概率值证明，被推进到了38%。

令这些数学家好奇的是，基于Gilmer的研究，他自己上手将概率值推进到38%并不难。

对此，Gilmer表示，自己已经五年多没碰数学了，确实不知道如何进行分析工作来将其进一步推进下去。

不过，他也认为，正是因为对相关数学方法的生疏，让他跳出了常理，用圈外办法取得突破。

深度学习界的万引大佬

虽说此前在数学界没什么名头，Justin Gilmer也并非等闲之辈。

他任职于谷歌大脑团队，Google Scholar上引用破万，主要研究方向为深度学习、组合型、随机图论。

从其研究成果看，Justin Gilmer主攻图神经网络，高引论文涉及：消息传递神经网络（MPNN）、关系归纳偏差与图神经网络、显著图等领域。

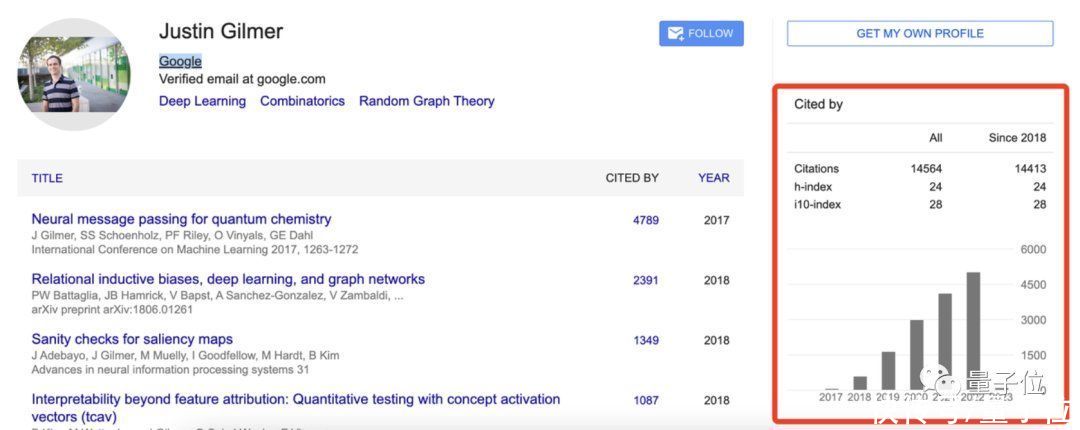
上述研究中，最高引用数为4789，标题为：Neural Message Passing for Quantum Chemistry。

该文定义了一种图上监督学习框架，消息传递神经网络（MPNN），并将其应用于分子特性预测上。

以量子化学为例，该框架根据原子性质（对应节点特征）和分子结构（对应边特征）预测了13种物理化学性质。

这一成果在领域内影响深远，腾讯AI Lab的云深智药平台，其框架之一也基于MPNN改进发展而来。

另值得一提的是，Justin Gilmer还到过中国北京，2007年夏天他在微软亚研短暂呆过3个月。

根据其领英账号，Gilmer当时在一个4人团队，参与构建SVM分类器，用于识别句子中人名、地名、机构名等各命名实体之间的关系。

参考链接：

— 完 —

量子位 QbitAI · 头条号签约

台海帖4437数学如何学习进步最快? -
汲菁畅18490452883 ______ 1.课前预习,对所学知识产生疑问,产生好奇心. 2.听课中要配合老师讲课,满足感官的兴奋性.听课中重点解决预习中疑问,把老师课堂的提问、停顿、教具和模型的演示都视为欣赏音乐,及时回答老师课堂提问,培养思考与老师同步性,提...

台海帖4437怎么样学数学最快?
汲菁畅18490452883 ______ 书山有路勤为径,学海无涯苦做舟,勤能补拙. 改善学习方法. 在学习过程中,一定要:多听(听课),多记(记概念,记公式),多看(看书),多做(做作业),多问(不懂就问),多动手(做实验),多复习,多总结. 相信你一定会逐渐养成良好的学习习惯,并获得成功. 对了,还要严格控制上网时间.

台海帖4437要怎样才可以较快速学好数学呢?
汲菁畅18490452883 ______ 想快速学好数学,首先你必须知道你在数学中哪一重点比较不好,哪一重点学得比较好.然后再根据你的自身条件,对你的相对弱点着重复习,对优势也要保持一定量的练习,在这段期间,你可以做数学练习资料,不要每题都过关,最重要的是资料上的例题,这些例题都是比较经典的,把握这些例题的做题技巧,你就可以解决很多你没见过的题型了.最后很重要的是你应该把握身边的同学,如果你不是很擅长交流,你就注意倾听,很多时候他们讲到的知识点刚好是你不了解或者根本就不记得的,在这个时候人的记忆力是很强的. 贵在坚持,希望采纳!

台海帖4437如何快速学习数学! -
汲菁畅18490452883 ______ 1. 培养学习兴趣2. 提高听课效率3. 课前预习,做好学习计划4. 课后多做题复习,巩固上课内容5. 不懂的要及时问明白,及时消化疑难问题6. 明确数学学科的重要性,学不好数学,以后考高中、大学继续深造 都困难重重

台海帖4437有什么方法可以快速学好数学啊
汲菁畅18490452883 ______ 一、课内重视听讲,课后及时复习. 新知识的接受,数学能力的培养主要在课堂上进行,所以要特点重视课内的学习效率,寻求正确的学习方法.上课时要紧跟老师的思路,积极展开思维预测下面的步骤,比较自己的解题思路与教师所讲有哪些...

台海帖4437怎样可以快速提高数学? -
汲菁畅18490452883 ______ 心态:了解数学,数学作为一种基础学科,任何学科都需要运用,数学不是特别的难,要认真的去对待; 2、 预习:学习过程主要是积累的过程,数学学的好不好,关键是自学能力的提高,课上的时间是有限的,老师也不会面面聚到的给每个同...

台海帖4437数学要怎么学才可以快速学好~
汲菁畅18490452883 ______ 学好数学首先要爱上数学,培养对数学的兴趣,例如上网搜看一些数学趣味的知识等等,逐渐培养对数学的兴趣,才会看见数学题不头疼.其次,课上不一定要每分钟都细听,要学会利用时间,学习关键的知识,不会一定要问,不要害羞等等.你要当学数学想玩一样,但不能不认真学.然后作业认真,课后还可以作数学游戏,杂志上都会有,或者开展数学趣味知识竞赛等、所以,学好数学不是一朝一夕,要逐渐养成,好的习惯和兴趣最多27天即可养成,不要害怕辛苦,其实数学是一个很有趣的科目,不要为了考试写作业而学数学,而要将它作为乐趣,在无聊时可以排解的伙伴,.祝你早日学好数学,天天开心!

台海帖4437怎样快速学好数学
汲菁畅18490452883 ______ 一、课本要“预、做、复”.每堂新课之前,做到先预习,特别要把难点或不懂之处用彩笔划出,以便上课时更加注意.每节内容后面的练习自己可以先做一做,做到看懂70%的新内容,会做80%的练习题.每节新内容学完后,我们要按照课本...