导数五步法画函数图像10个函数示意图应用举例之一
\n\n
\n\n
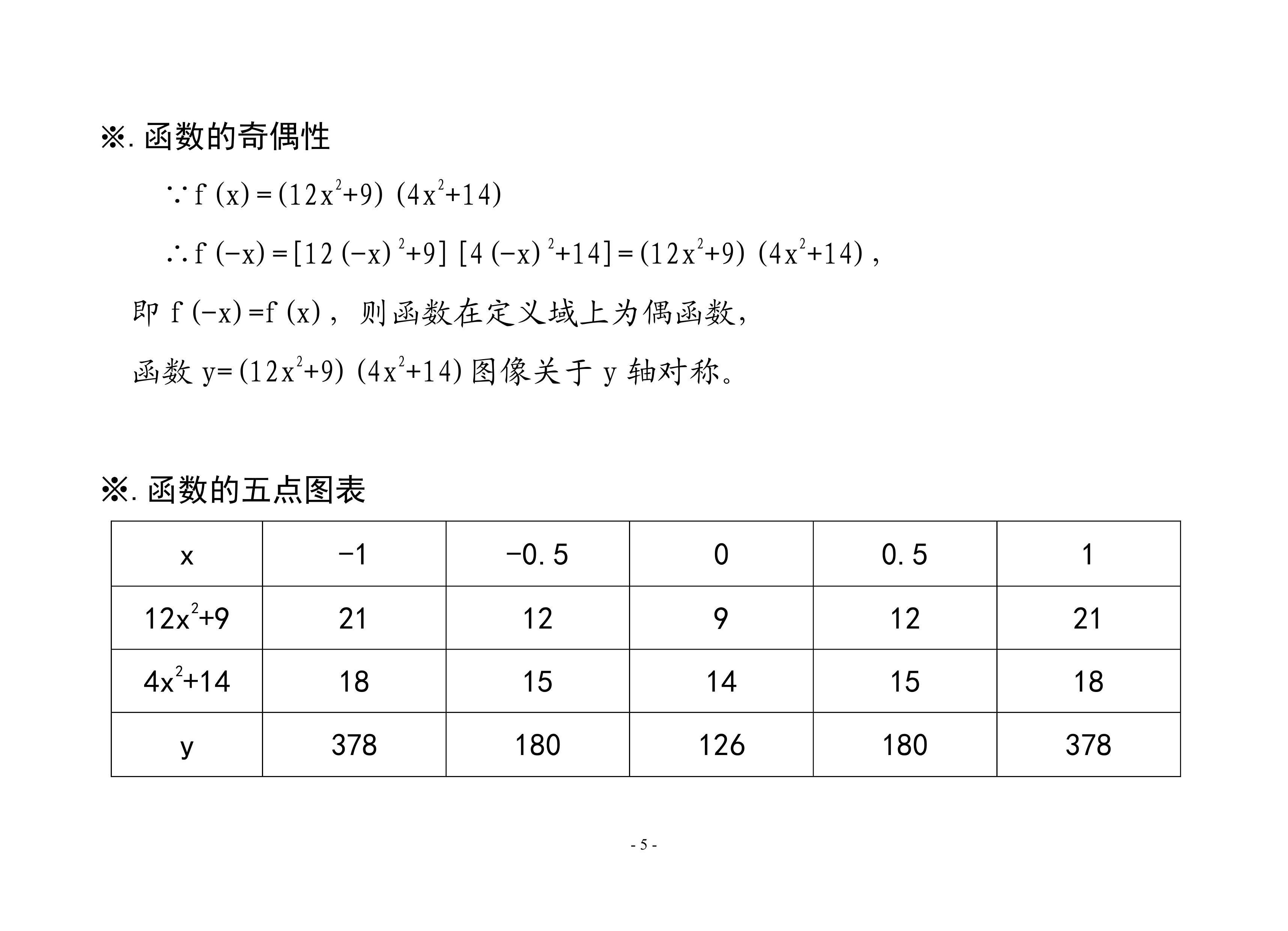
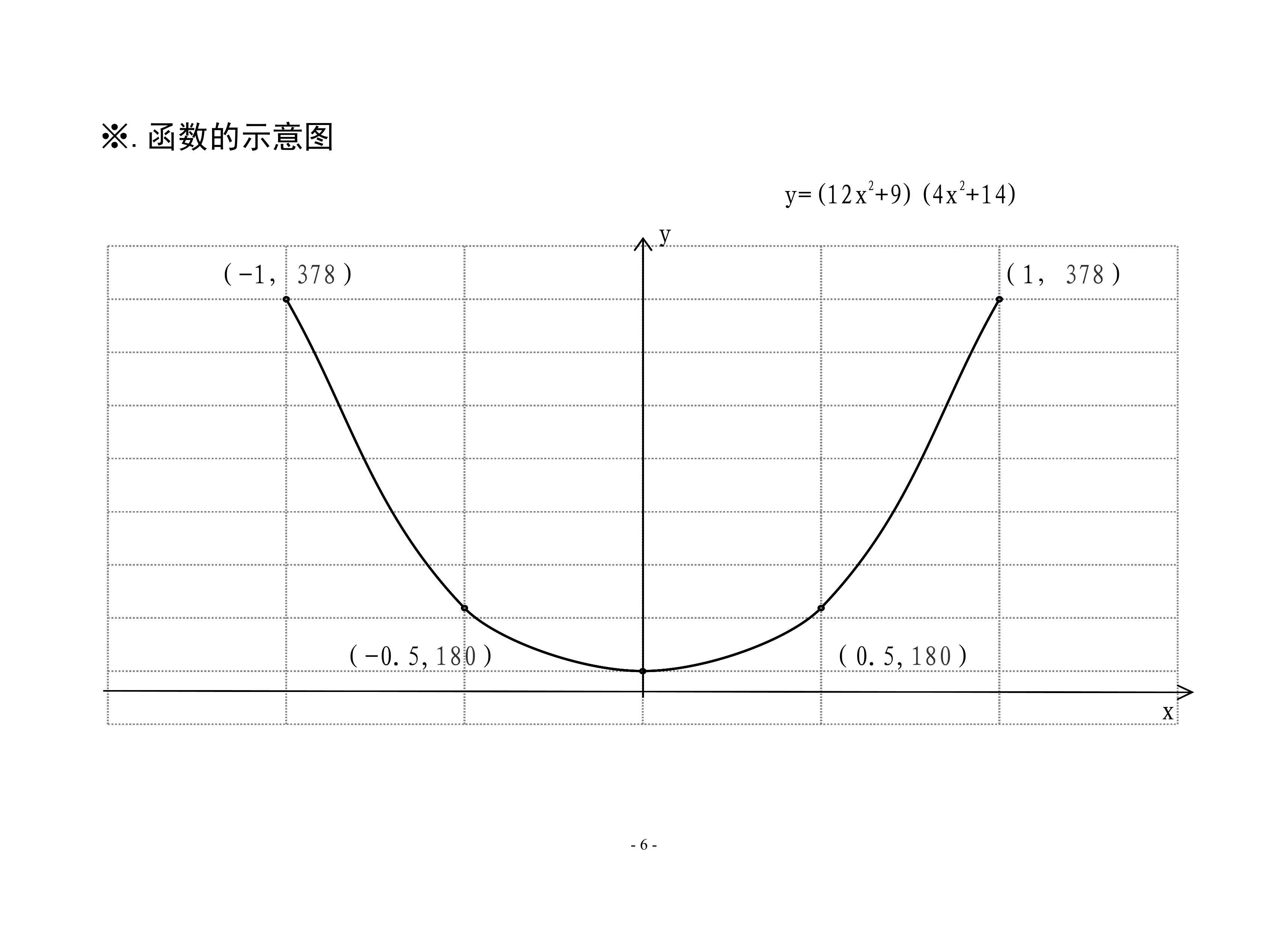
1.函数y=(12x2+9)(4x2+14)的图像示意图:介绍函数的定义域、单调性、凸凹性、极限等性质及五点图表,并通过导数知识计算函数的单调和凸凹区间,简要画出示意图。
\n\n
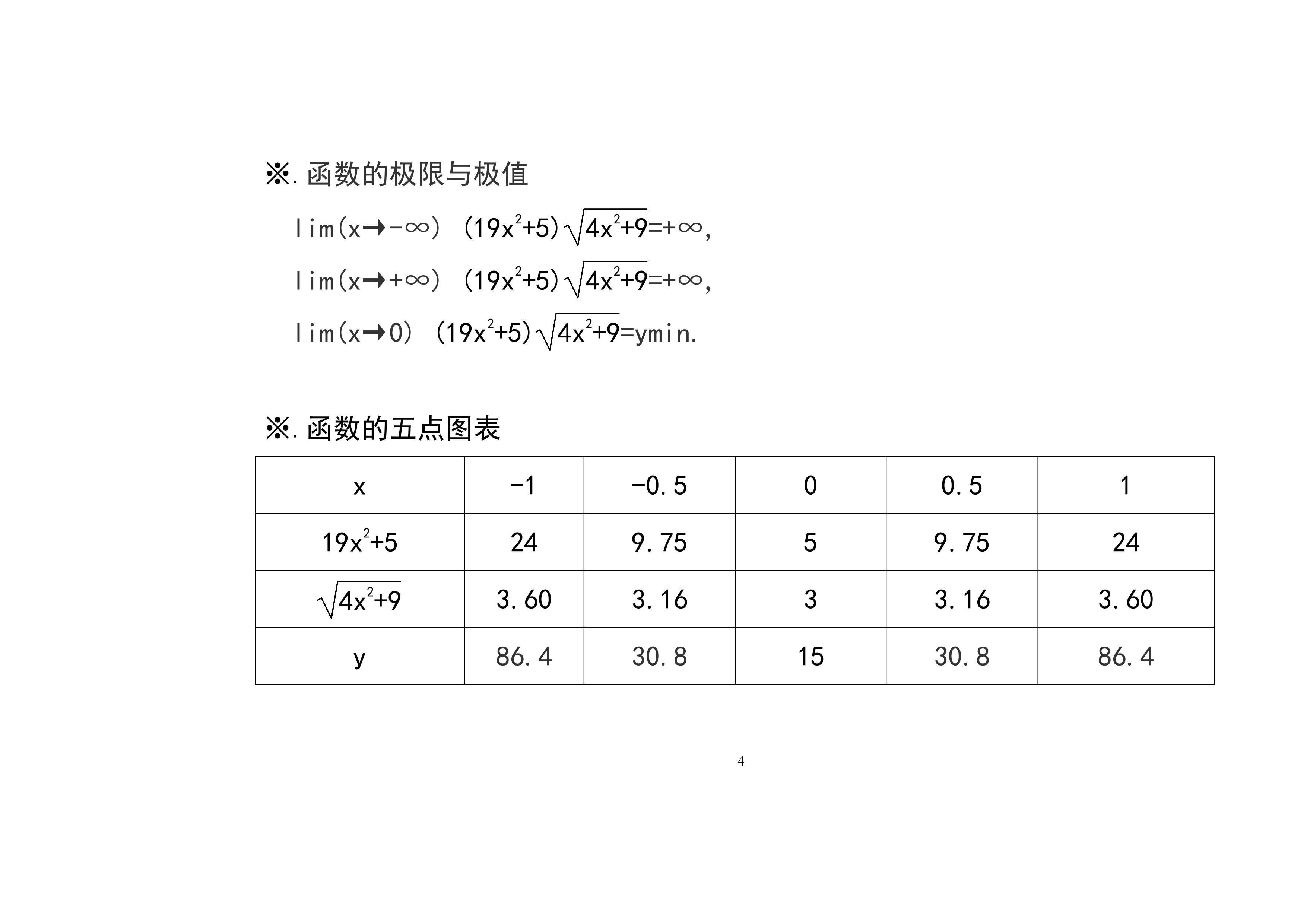
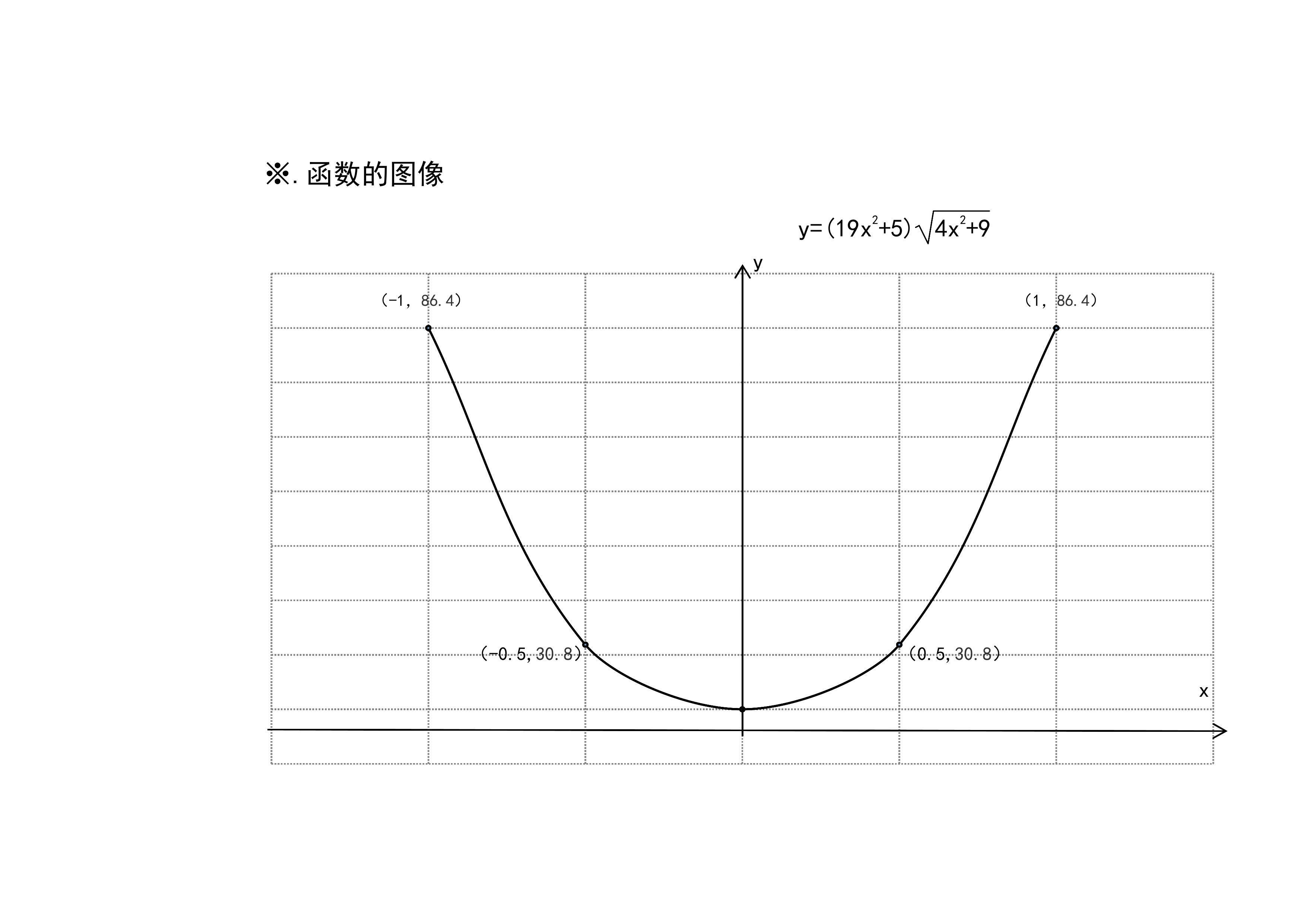
2.函数y=(19x2+5)√(4x2+9)的主要性质及其图像:介绍函数的定义域、单调性、凸凹性、极限等性质,列举函数的五点图表,进一步画出函数的示意图。
\n\n
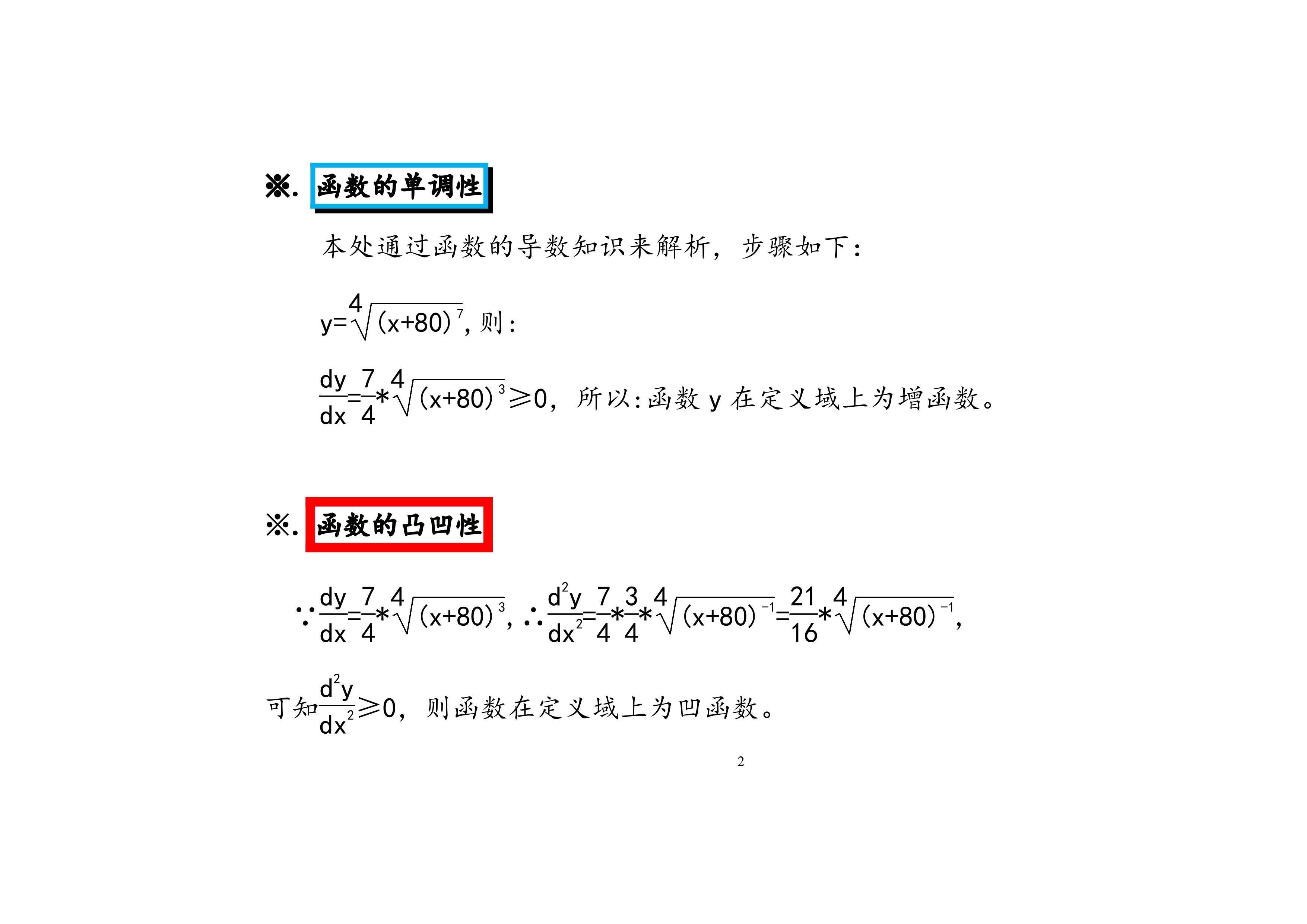
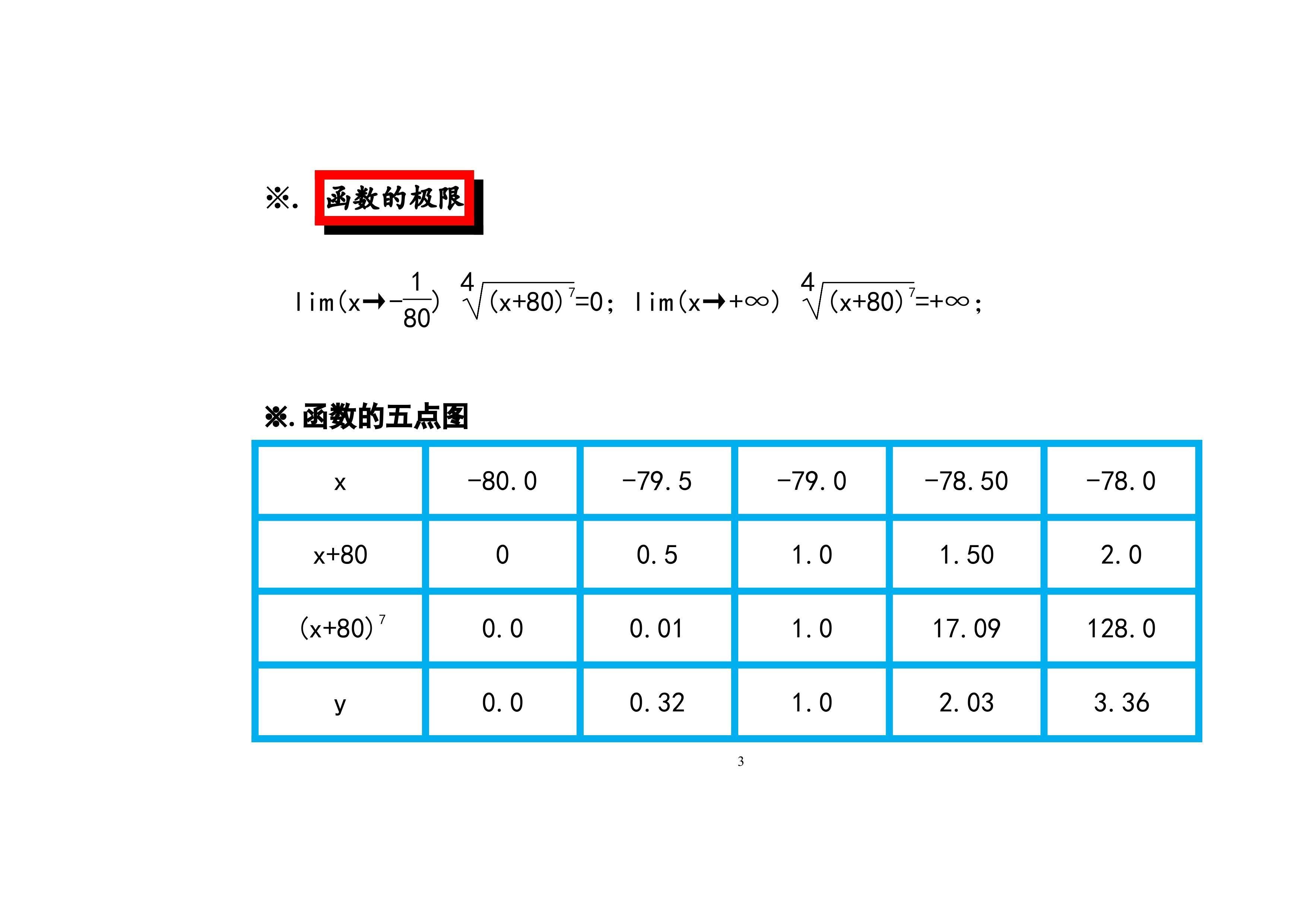
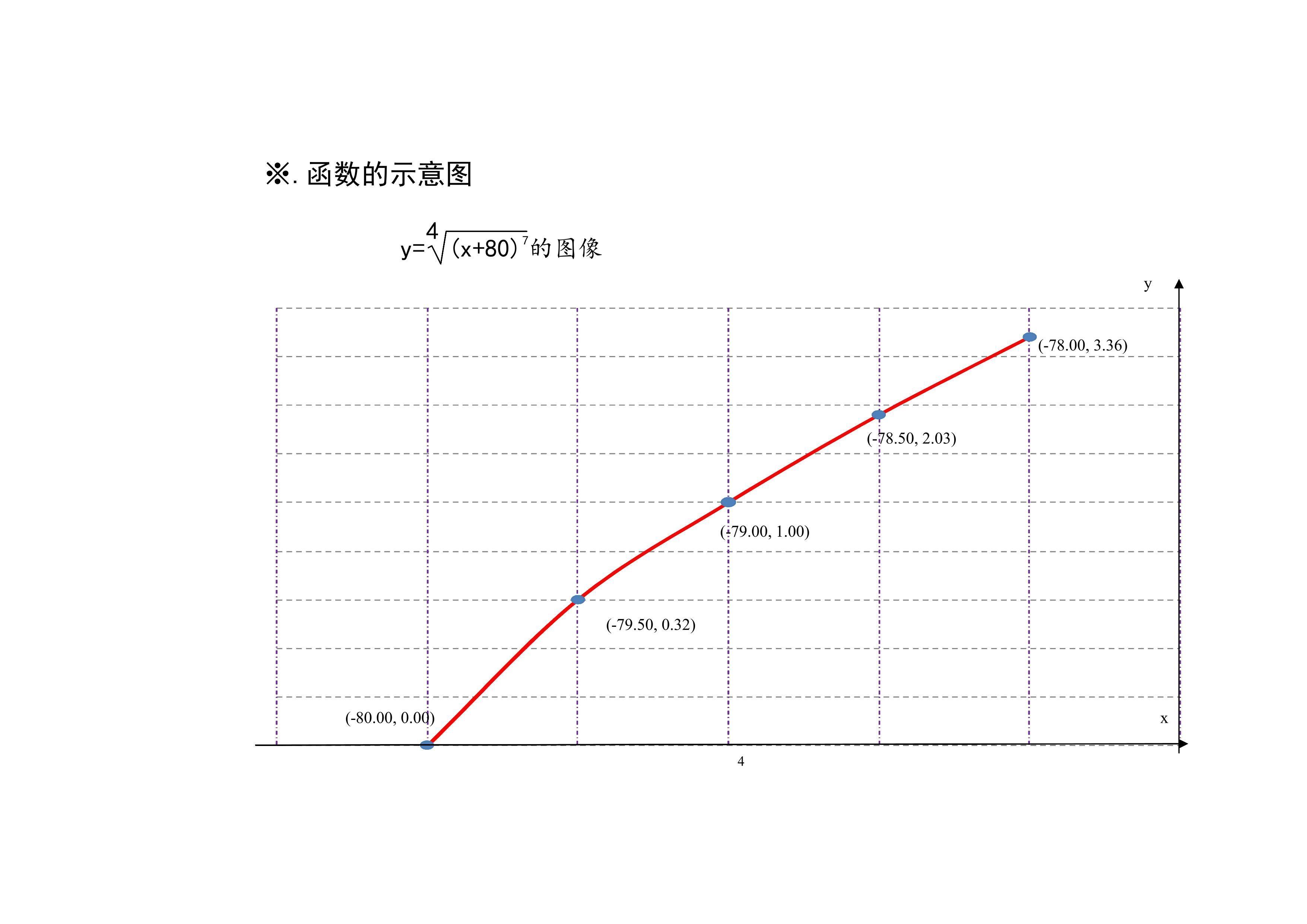
3.函数y=4√(x+80)^7图像画法及步骤:本文通过函数的定义、单调、凸凹性和极限等性质,介绍函数的主要性质及图像画法步骤。
\n\n
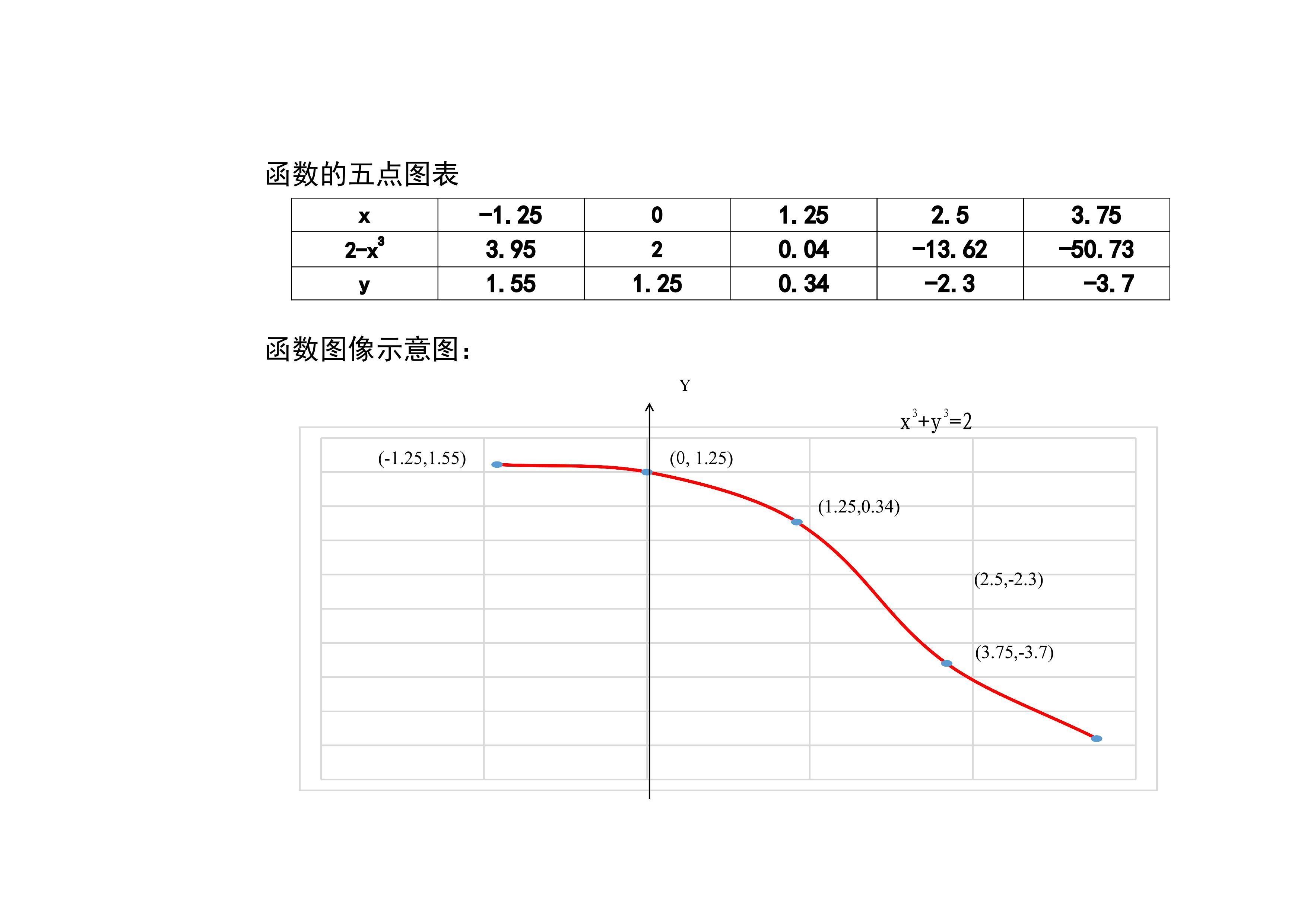
4.曲线x³+y³=2的主要性质及其图像示意图:介绍曲线方程的定义域、单调性、凸凹性等性质,同时用导数的知识求解函数的单调区间和凸凹区间,并简洁画出函数的图像示意图。
\n\n
5.√(x+4)+√(3y+5)=2的图像示意图:介绍曲线方程的定义域、单调性、凸凹性及极限等性质,同时用导数简洁画出函数的图像示意图。
\n\n
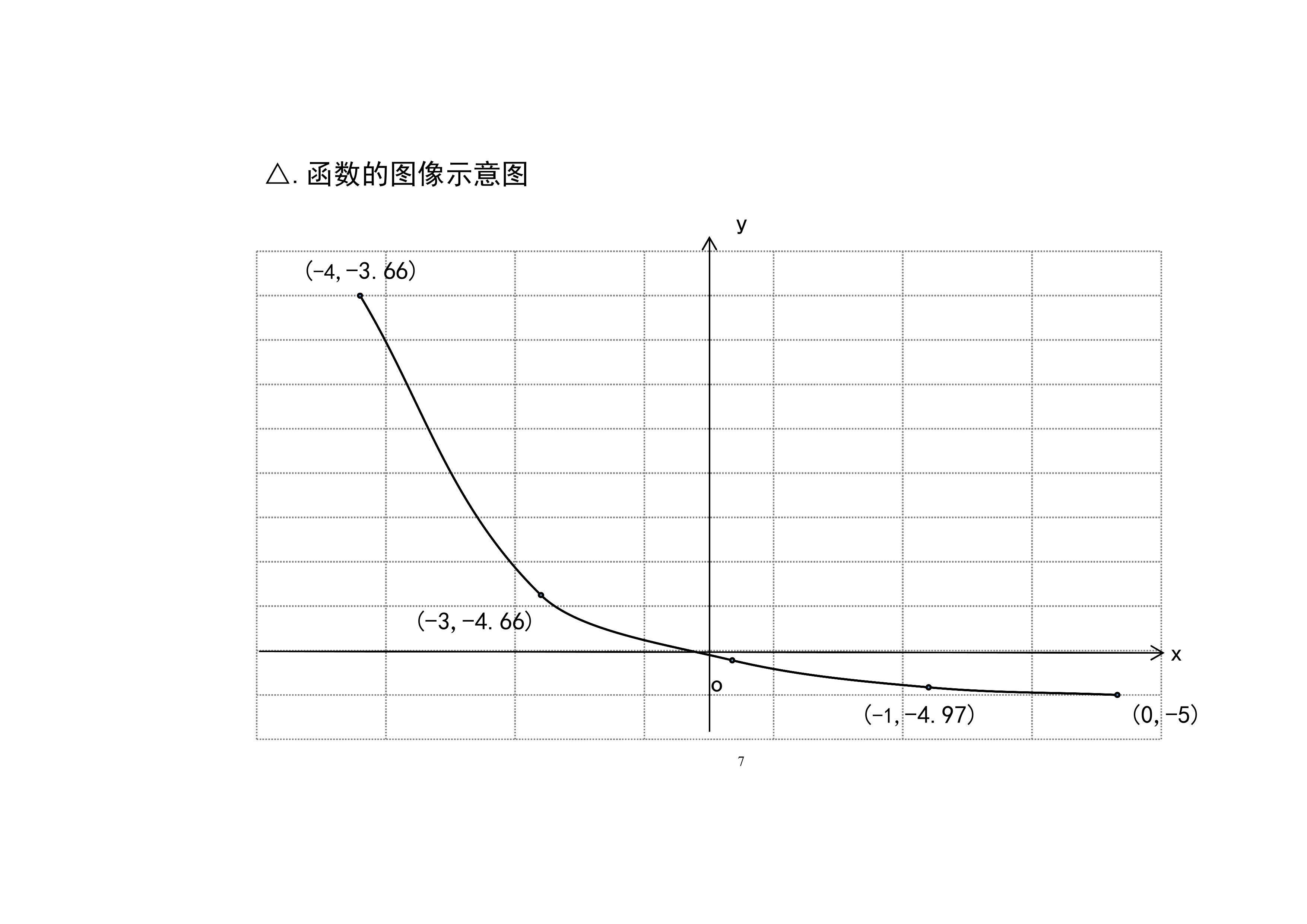
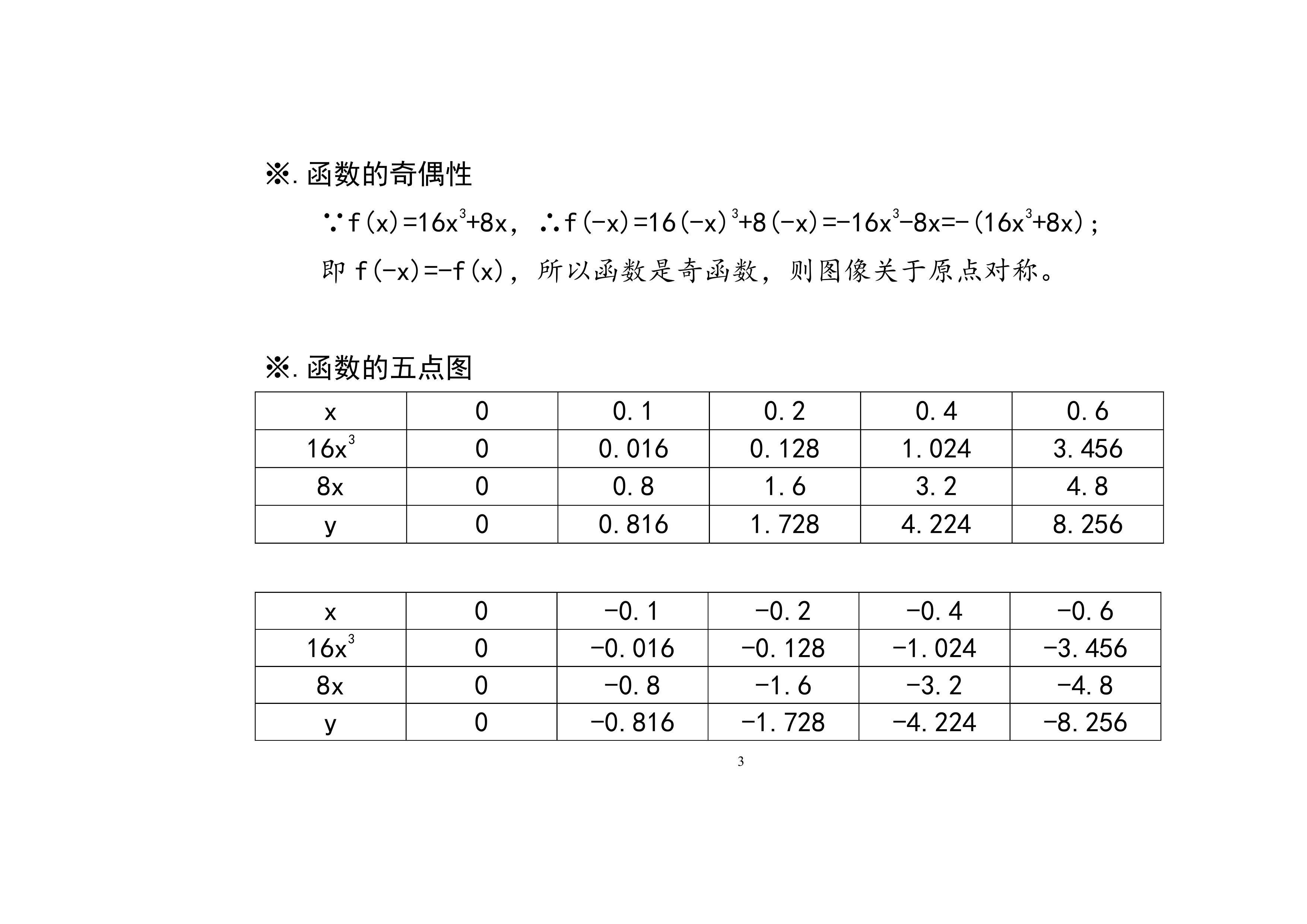
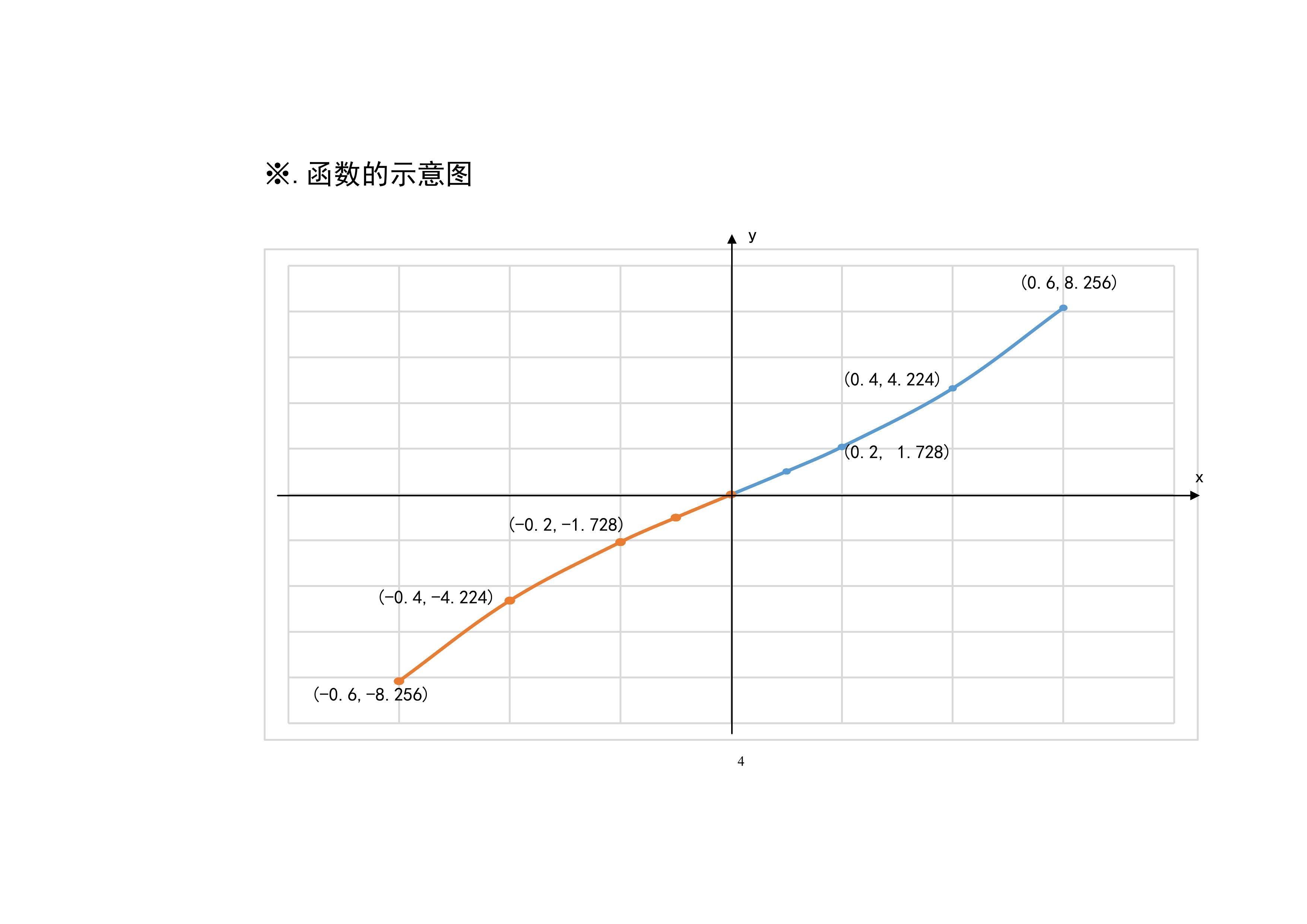
6.函数y=16x3+8x的图像示意图及主要性质:介绍函数的定义域、单调性、凸凹性、极限等性质,列举函数的五点图表,进一步画出函数的示意图。
\n\n
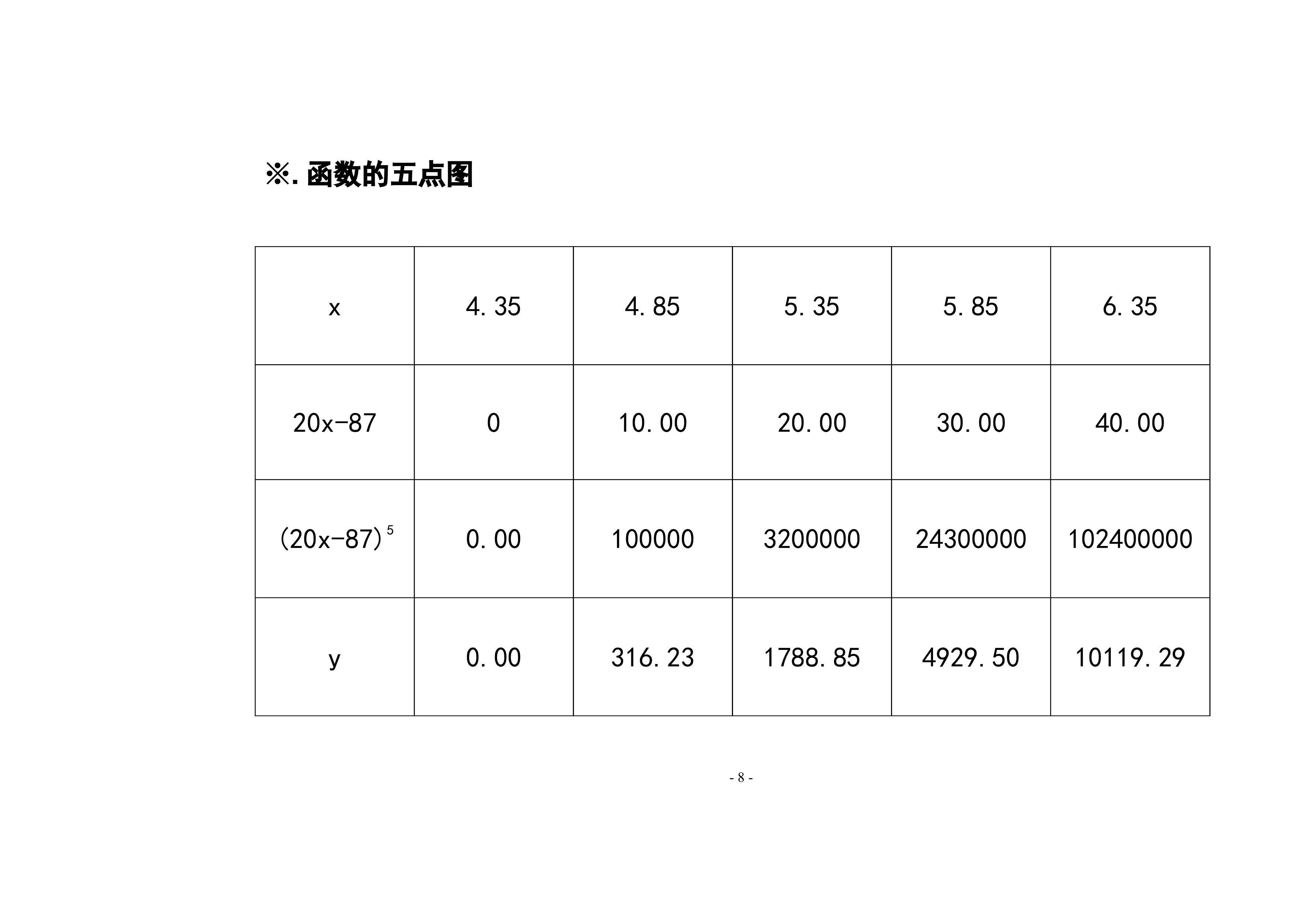
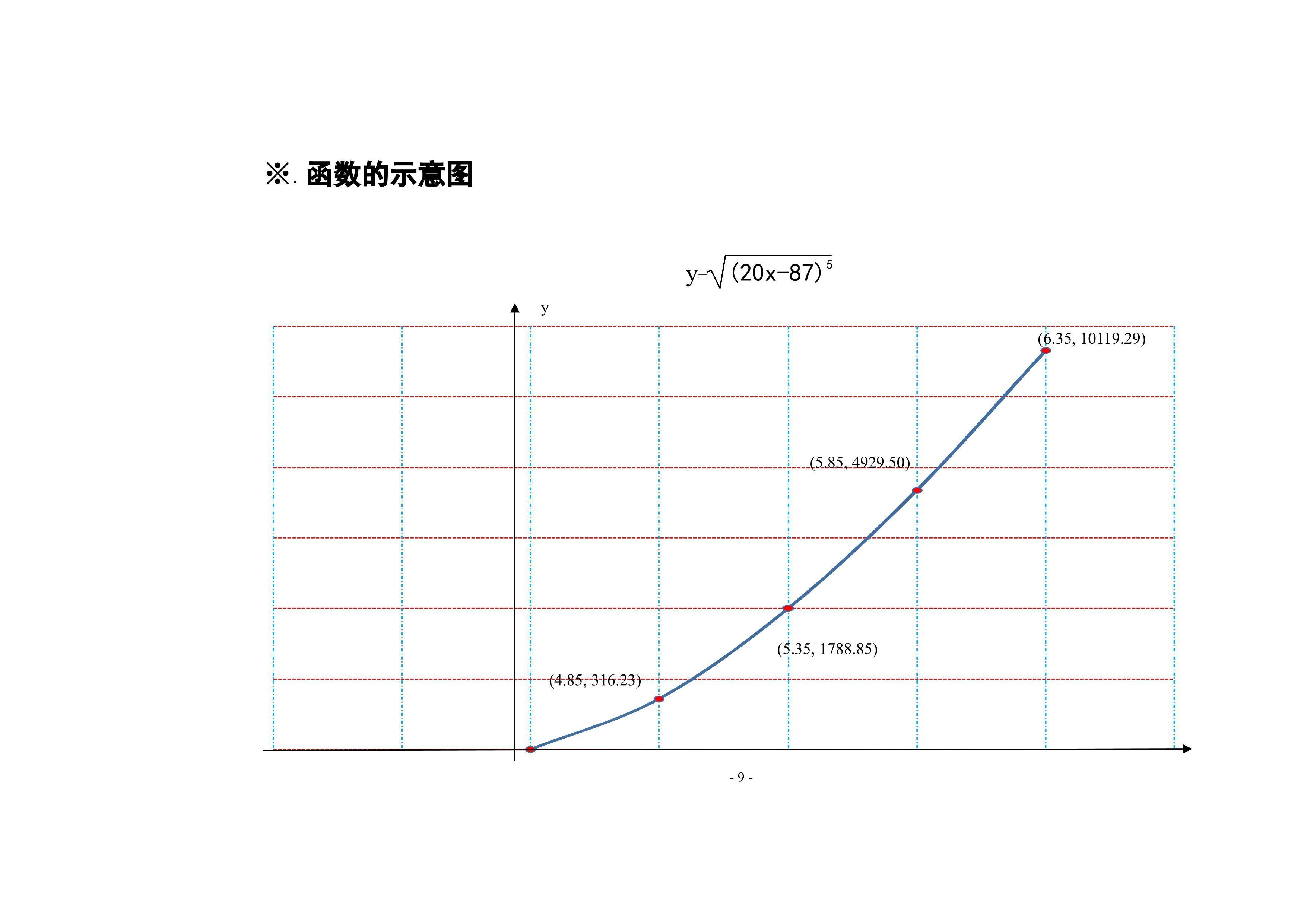
7.函数y=√(20x-87)^5图像画法及步骤:通过函数的定义、单调、凸凹和极限等性质, 并通过导数知识,介绍函数的主要性质及图像示意图画法步骤。
\n\n
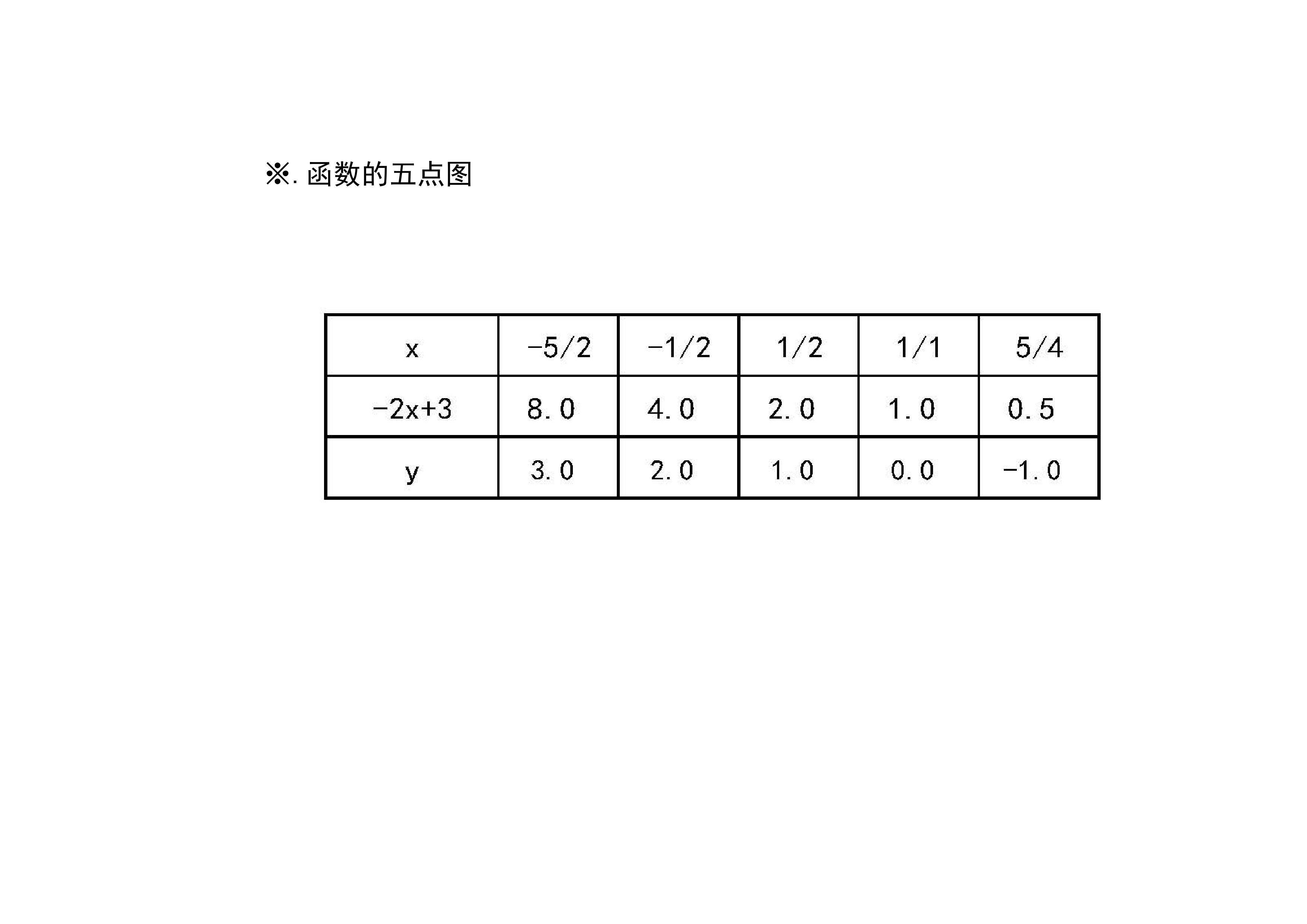
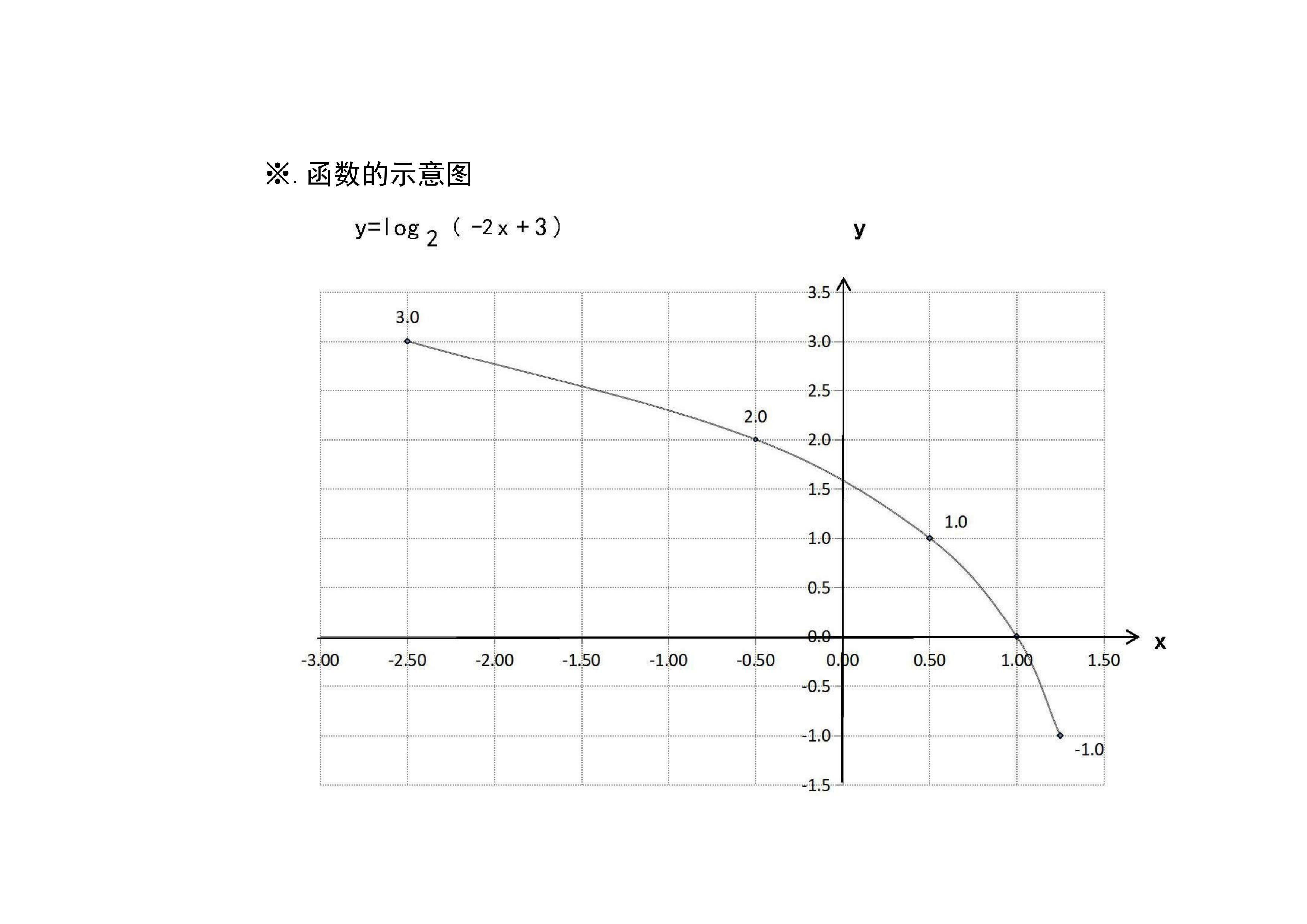
8.函数y=log2(-2x+3)的图像示意图:介绍函数的定义域、单调性、凸凹性、极限等性质,列举函数的五点图表,简要画出函数的示意图。
\n\n
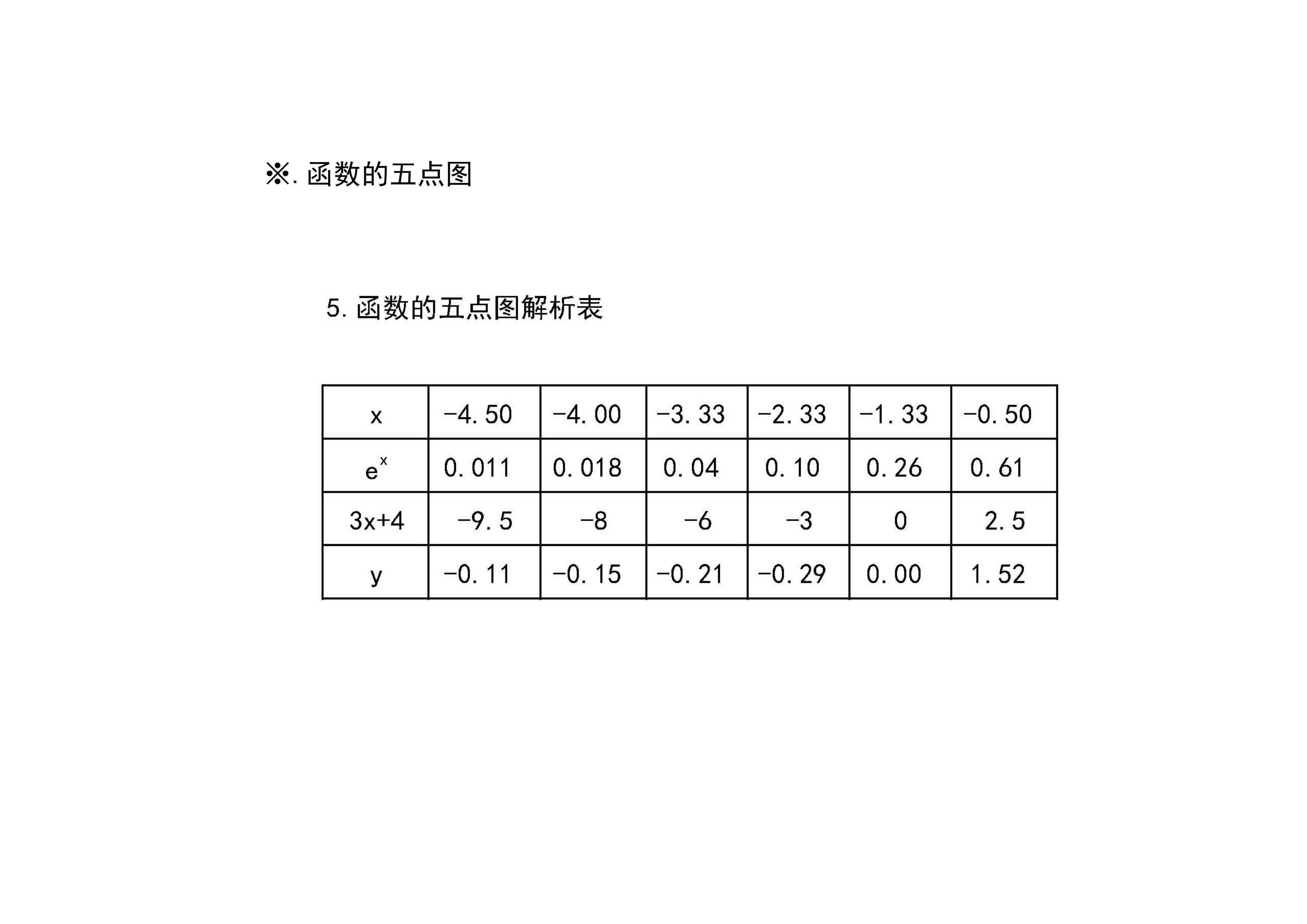
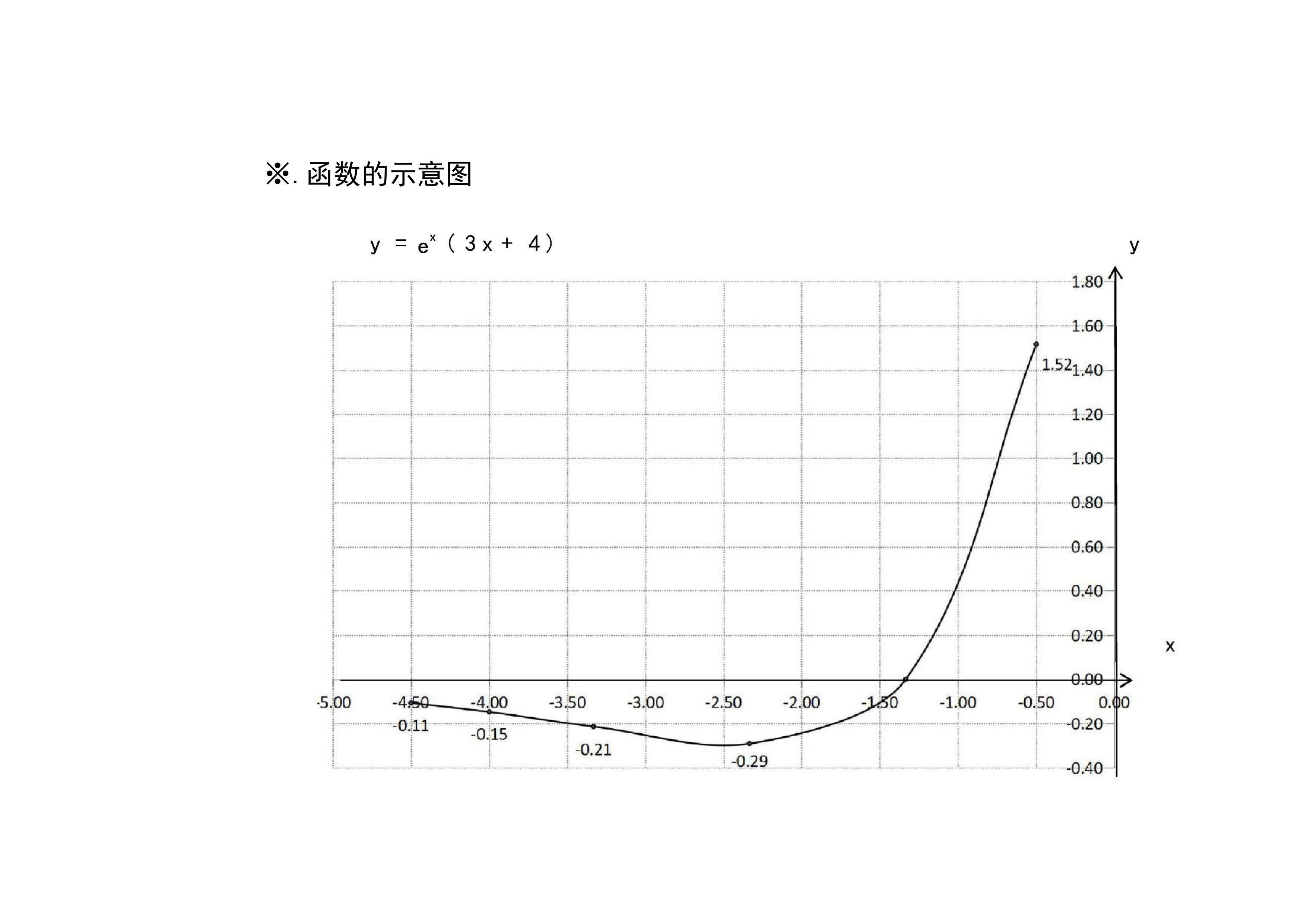
9.函数y=e^x(3x+4)的图像示意图:本文通过函数的定义、单调、凸凹性和极限等性质,介绍函数的主要性质及图像画法步骤。
\n\n
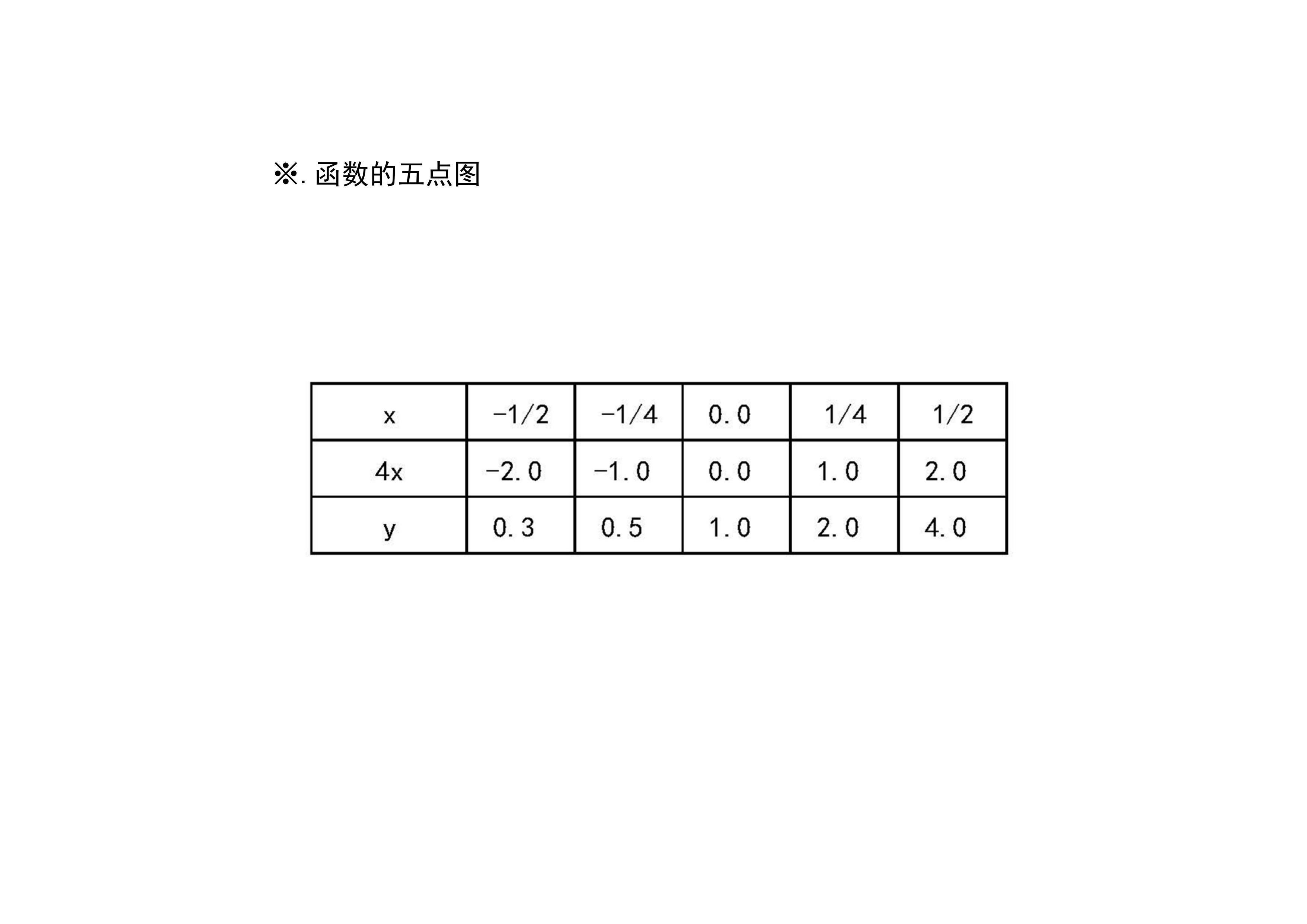
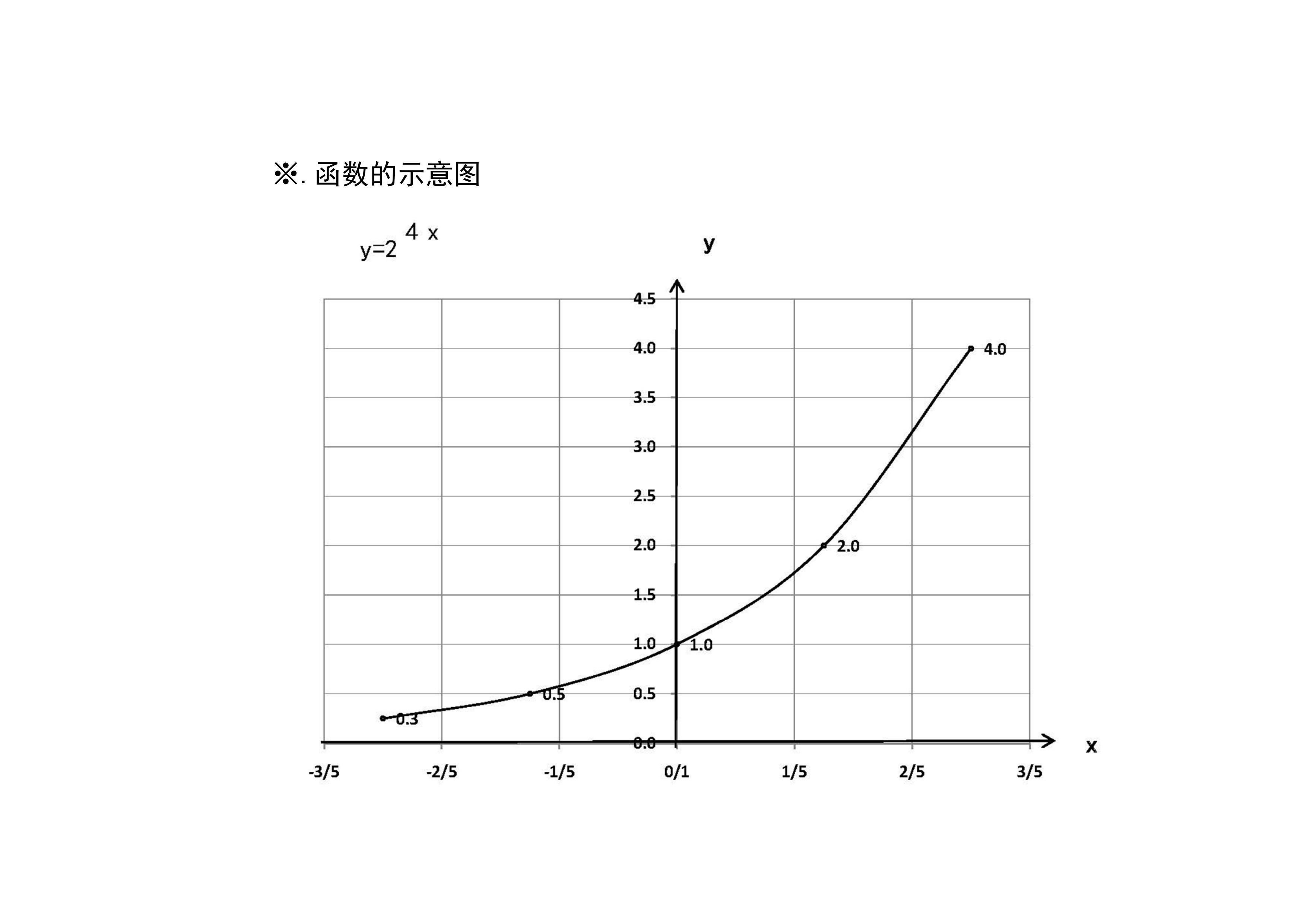
10.函数y=2^4x的图像示意图:介绍函数的定义域、单调性、凸凹性、极限等性质,列举函数的五点图表,进一步画出函数的示意图。
\n\n
\n\n
































","gnid":"9758824ec7671aa4d","img_data":[{"flag":2,"img":[{"desc":"","height":925,"title":"","url":"https://p0.ssl.img.360kuai.com/t01a370aba0dc0184ae.jpg","width":1280},{"desc":"","height":925,"title":"","url":"https://p0.ssl.img.360kuai.com/t01fe729509bf6963a8.jpg","width":1280},{"desc":"","height":925,"title":"","url":"https://p0.ssl.img.360kuai.com/t01c644eeab94a0efe6.jpg","width":1280},{"desc":"","height":925,"title":"","url":"https://p0.ssl.img.360kuai.com/t013539215e0a83c2a4.jpg","width":1280},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t011ac510957e2c014e.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01b6300bde0321b12c.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t010ec62f9edc968eba.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t012ea8cadd7067c59a.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0135e6b9e5ad5f2723.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0101a95b931e2c6661.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0156869fd05f1b9bb9.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01eeb16f6ae9877b62.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01fd234f62dc83b806.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01a7177f0c14cf1b67.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01f3e9bcbfa66207be.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0111341fafd83e8b23.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01b12ae4529c0fc1a5.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01c2d414e70ce33022.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01a6435466e13d89c7.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0179a153481db89522.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t013f7979ab67311565.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t012871721b42a710c1.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t013b8fb94c7da143c9.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t015c6380a9e4dd5da4.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01c8edbb39b9d7fe87.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0122b1ab788e519a35.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01b446dfdddb35e4bf.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01651411583c303362.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0126094f1ca9ed1956.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t018fabf5214cdfc785.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t015b3f1e97b4dbe1ae.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01190830f3a32242fd.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01f1055028c526dd9d.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01e3ef63beab75c785.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t011dde9de6ce8a849b.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t019e8dbf2156e3031f.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t017d660aed63d492fa.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t017d660aed63d492fa.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0173f2a15f98505230.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0121e883d03506ad7f.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01fd20ffaf7942432d.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0174518a47ce9dd664.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t013e8e7b19fa695693.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0130fe2d9574be5db9.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0143c4b32aae3b438c.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01f74b752f697884fa.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0117c554a911c21419.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t0141cfbe536892d640.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01d396d571728906e5.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t01c87a38b737bd03fb.jpg","width":"3509"},{"desc":"","height":"2481","title":"","url":"https://p0.ssl.img.360kuai.com/t018eaaf25c81dbece5.jpg","width":"3509"}]}],"original":0,"pat":"pdc,art_src_0,fts0,sts0","powerby":"cache","pub_time":1711495200000,"pure":"","rawurl":"http://zm.news.so.com/7339c860ffebb01ebf215d79eb02f630","redirect":0,"rptid":"65e62da3ddba0208","rss_ext":[],"s":"t","src":"仁新数学","tag":[],"title":"导数五步法画函数图像10个函数示意图应用举例之一
令钢程4563y= e^ x是什么函数,怎么求图像和性质呢? -
虞码何18375493871 ______ y=e^x是指数函数.y等于e的x次方是一种指数函数,其图像是单调递增,x∈R,y>0,与y轴相交于(0,1)点,图像位于X轴上方,第二象限无限接近X轴.在指数函数的定义表达式中,在ax前的系数必须是数1,自变量x必须在指数的位置上,且不...
令钢程4563y=ex分之一的定义域是 -
虞码何18375493871 ______[答案] 若是y=e^(1/x),那么定义域是{x|x≠0}; 若是y=1/(e^x),那么定义域是R
令钢程4563lnx的值域为什么是R?我知道定义域是0到正无穷,举个负数的例子! -
虞码何18375493871 ______[答案] 它是y=e^x的反函数,它的值域就是y=e^x的定义域,也就是R
令钢程4563函数y=e^│x│/x的图像大致是: -
虞码何18375493871 ______[答案] y=f(x)=e^│x│/x定义域x∈R,x≠0f(-x)=e^|-x|/(-x)=-e^|x|/x=-f(x)∴f(x)是奇函数,图像关于原点对称当x>0时,f(x)=e^x/xf'(x)=e^x(x-1)/x∴01,f'(x){...
令钢程4563函数y=e^x+sin(x^2 - 1)/ln(x+3)的定义域是 -
虞码何18375493871 ______[答案] x+3>0,且ln(x+3)≠0 得:x>-3且x≠-2 所以,定义域为(-3,-2)U(-2,+∞)
令钢程4563y=e^ - x的定义域是多少?这是y等于e的负x次方 -
虞码何18375493871 ______[答案] R
令钢程4563y=u^3. u=tanv. v=e^x - 1. 求出它们的定义域 -
虞码何18375493871 ______ 1、v=e^x-1 定义域 x ∈ R2、u=tanv,定义域{v|v≠kπ+π/2} k∈Z,e^x-1≠kπ+π/2,e^x≠kπ+π/2+1,x≠ln(kπ+π/2+1) k∈Z3、y=u³,u∈ R,定义域 x≠ln(kπ+π/2+1) k∈Z
令钢程4563函数y=e^x - 1的反函数是 反函数的定义域是 -
虞码何18375493871 ______[答案] y+1=e^x log以e为底y+1的对数=x 也就是y=log以e为底x+1的对数是反函数. 定义域是(-1,+穷)
令钢程4563函数y=根号e^x - 1的定义域是, -
虞码何18375493871 ______[答案] y=√(e^x-1) 函数有意义,需 e^x-1≥0 即e^x≥1=e^0 ∴x≥0 函数定义域为[0,+∞)


















































