交错级数不递减反例

陶哲轩又发新论文了！

这也是时隔一年，他再次独立发表新论文。（arXiv显示上一篇独作论文发表时间是在去年2月）

这篇新论文依旧与陶哲轩钻研的数论领域有关。

它证明了著名数学家埃尔德什·帕尔（Erdős Pál）提出的一个交错素数级数猜想，在哈代-李特尔伍德素数k元组猜想成立的条件下，是成立的。

（当然，哈代-李特尔伍德素数k元组猜想也是一个悬而未解的猜想，因此这项研究只是部分证明，并没有完全解决）

这项研究，还用到了他在几年前与合作者共同提出的一个素数随机模型。

一起来看看。

证明了什么样的猜想？

核心来说，这篇新论文要证明的，是埃尔德什提出的一个关于交错素数级数收敛性的猜想。

这个猜想与一个长这样的交错级数有关，其中pn是第n个素数：

但交错级数并不一定收敛，因此需要具体级数具体判断，这次陶哲轩证明的就是交错级数中的一个特殊类型，即an是素数pn的倒数，这个级数是收敛的。

不过，还有个前提条件——在哈代-李特尔伍德素数k元组猜想成立的条件下。

哈代-李特尔伍德素数k元组猜想，由英国科学家哈代和李特尔伍德提出，它预测了给定差值集合的k个素数出现的频率。

猜想认为，存在两个绝对常数ε>0和C>0，对于所有x≥10、所有k≤(log log x)^5、和所有由不同整数h1,…,hk组成的k元组：

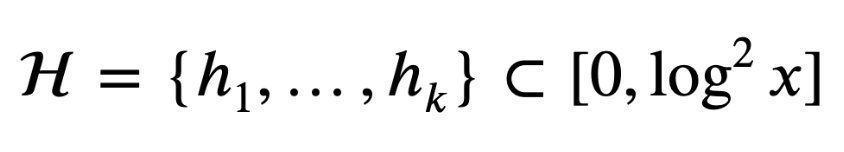
使得这个式子成立：

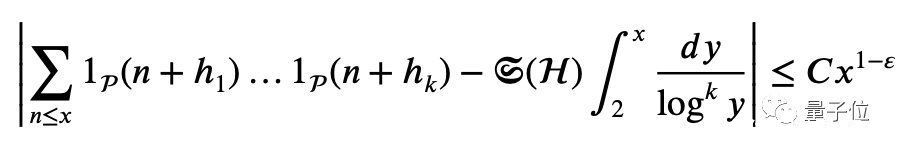
不过，这个猜想至今尚未解决。

这次陶哲轩直接在假设它成立的基础上，证明了交错素数级数收敛性猜想的成立。整个过程大约可以分为四步：

首先，基于Van der Corput差分定理来降低素数计数间隔的长度。

由于证明这个猜想，实际上需要估计区间[1,x]内素数个数的奇偶性分布，因此使用差分定理的目的，能将它转化为仅考虑较短区间内素数个数奇偶性的问题。

转化为这个问题之后，实际上就能用哈代-李特尔伍德素数k元组猜想来证明问题成立。

因此，接下来论文在假设哈代-李特尔伍德素数k元组猜想成立的基础上，估计了短区间内k个素数的概率。

然后，陶哲轩使用几年前与两位数学家William Banks和Kevin Ford共同建立的随机素数模型，来建模素数分布。

最后基于这个模型建立的分布证明猜想。

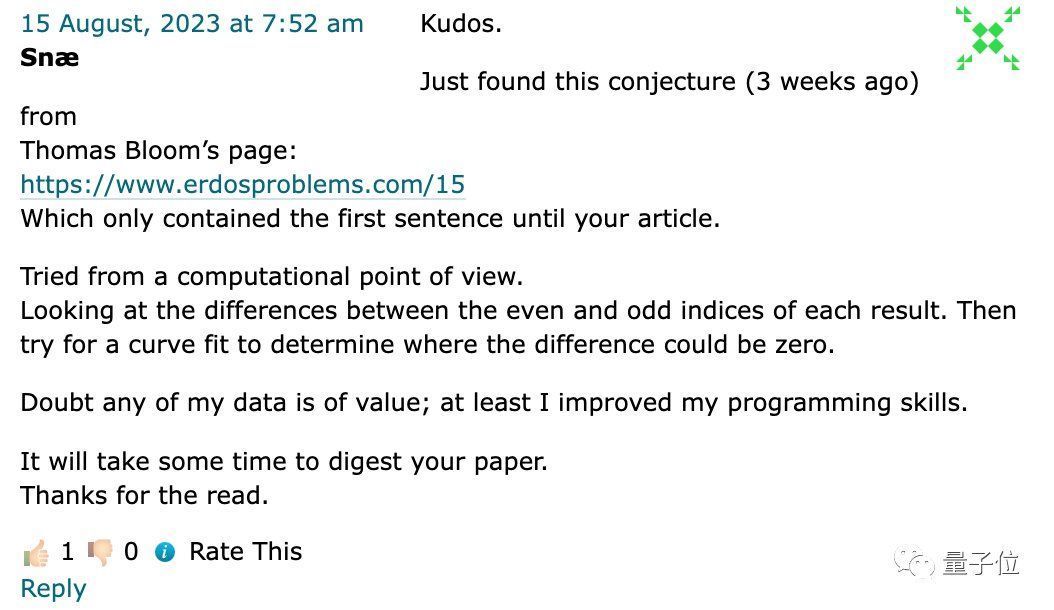
这篇博客发出后不久，就有网友赶来点赞，表示自己也在从用另一种方法尝试解决这个猜想：

One More Thing

值得一提的是，2004年陶哲轩和本·格林（Ben Joseph Green）提出的著名格林-陶定理，也是基于埃尔德什·帕尔（Erdős Pál）另一个更著名的等差数列猜想而来。

其中，埃尔德什等差数列猜想如下：

格林-陶定理进一步将猜想范围缩小到他们研究的素数范围内，相当于埃尔德什等差数列猜想的一个“特例”：

埃尔德什为解决这个等差数列猜想悬赏了5000美元。

这些年除了陶哲轩以外，也有不少数学家致力于它的研究，例如Thomas Bloom和Olof Sisask。他们在2020年，证明了整数无穷数列一定包含长度至少为三的等差数列，将这个问题又向前推进了一步。

感兴趣的小伙伴们可以挑战一下了（手动狗头）

新论文地址：

参考链接：

— 完 —

量子位 QbitAI · 头条号签约

姚航琪1960无穷级数的问题如果一个级数是发散的,那么去掉这个级数的级数奇数项或是偶数项所得到的新级数仍然是发散的吗? -
傅毓琴17745481294 ______[答案] 不一定

姚航琪1960高等数学,要判断该级数的收敛性,指出是绝对收敛还是条件收敛 -
傅毓琴17745481294 ______ 第三题过程证错了,n趋近无穷大时,lnN/n 极限为0 .这个级数为交错级数,可用交错级数定义证明,看f(x)=lnx/x 是否递减,求导可知,x>e,函数递减.故原级数条收敛. 针对第四题,因为级数an(an为大于等于0)收敛,故0<=an^2<=an,由于级数an收敛,故级数an^2也收敛.这个级数不会让判断绝对与条件收敛吧,因为都是大于0的级数,要么收敛,要么发散

姚航琪1960交错级数( - 1)^n*(n+1)/(3n - 2)是否收敛,如何证明 -
傅毓琴17745481294 ______[答案] 不收敛. 通项(-1)^n * (n+1)/(3n-2)的绝对值(n+1)/(3n-2) ->1/3,所以通项不趋向于0,级数不收敛. 注:对于交错级数(-1)^n * an,数列an递减,那么其收敛的的充要条件是an->0,这个条件一定要注意验证

姚航琪1960交错级数 高等数学求教根据莱布尼兹法则,交错级数满足两个条件:1.Un≥Un+1(n=1,2,3…),2.limUn=0则收敛.我的问题是,若条件一为Un≥Un+1(n≥e)即U1 -
傅毓琴17745481294 ______[答案] 你的问题的表达有点问题啊.我理解的意思是,第一个条件不是从n=1开始就成立,是吧?这个不影响交错级数的收敛性,因为级数的性质说了,去掉级数的有限项,不改变级数的收敛性.

姚航琪1960若级数∑an收敛,则级数∑an^2 必收敛 -
傅毓琴17745481294 ______ 未必.例如 an = [(-1)^n]/√n,则交错级数 ∑an 收敛,但级数 ∑an^2 = Σ(1/n) 是调和级数,是发散的.

姚航琪1960怎么判断级数是条件收敛还是绝对收敛?方法和步骤是什么? -
傅毓琴17745481294 ______[答案] 1:先判断是否收敛. 2:如果收敛,且为交错级数,则绝对收敛. 其实就是交错级数如果加绝对值收敛则为条件收敛,如果交错级数不加绝对值也收敛,则为绝对收敛.

姚航琪1960交错级数不满足莱布尼茨定理是发散的吗 -
傅毓琴17745481294 ______ 交错级数的莱布尼茨定理是充分条件不是必要的,不满足该定理可能可以用别的判别法来判别,不能直接判定是发散的;但如果通项不以零为极限,则发散是肯定的.

姚航琪1960高数 p级数 交错级数 -
傅毓琴17745481294 ______ p<0时,lim 1/n^p=lim n^(-p)=∞,一般项极限不是0,发散; p=0时,lim 1/n^p=1,一般项极限不是0,发散; 0<p<=1时,用莱布尼兹判别法知级数收敛,加绝对值后,变为Σ(1/n^p), 由于1/n^p≥1/n,且Σ(1/n)发散,由比较判别法,知级数发散; p>1时,级数加绝对值后为:Σ(1/n^p),该级数收敛,因此原级数绝对收敛. p>1时的收敛性证明书上有,这个不需要掌握,但结论要记住.

姚航琪1960无穷级数的交错级数 - 收敛性
傅毓琴17745481294 ______ 用莱布尼茨的时候,不是考虑{|an|}的单调性,而是考虑{an},要保证{an}递减趋于0,才能用莱布尼茨 但是这个数列显然不加绝对值cosnπ会正负交错,不单调

姚航琪1960交错级数具有什么性质呢?
傅毓琴17745481294 ______ 交错级数具有一个简单的性质:如果为一个单调递减数列,并且以0为极限,那么通过改变这个数列相邻两项的符号而构造的两个交错级数都收敛