基本不等式教材教学视频

物理学是一门探索自然界规律的科学,它涉及到从微观到宏观的各种现象。在物理学的发展历史中,有一些实验结果引起了人们的极大关注,它们不仅挑战了我们对物理世界的认知,也激发了我们对物理学本质的探索。其中一个典型的例子就是贝尔不等式。
贝尔不等式是由爱尔兰物理学家约翰·斯图尔特·贝尔(John Stewart Bell)在1964年提出的一种数学公式,它用来检验量子力学中一个非常奇特的现象——量子纠缠。量子纠缠是指两个或多个粒子之间存在着一种超越时空距离的联系,即使它们相隔很远,它们的状态也会同时改变。这种现象与我们日常经验中的物理规律相悖,也与经典物理学中的因果关系相违背。
贝尔不等式试图解释量子纠缠是否存在“隐藏变量”,即一些未被观测到的经典属性,来说明量子纠缠的行为。如果存在隐藏变量,那么量子纠缠就可以用经典物理学来描述;如果不存在隐藏变量,那么量子纠缠就是一种真正的非经典现象,需要用量子力学来解释。
本文将带您一起揭开贝尔不等式的神秘面纱,探索其背后的原理和意义。

要了解贝尔不等式,我们首先需要了解量子纠缠是什么。量子纠缠是指两个或多个粒子之间存在着一种特殊的关联,使得它们共享一个量子态。这意味着当我们测量其中一个粒子时,我们就可以知道另一个粒子的状态,即使它们之间没有任何物理联系。例如,如果两个粒子是纠缠的,并且它们都有一个属性叫做自旋(spin),那么当我们测量其中一个粒子的自旋时,我们就可以确定另一个粒子的自旋是相反的。这种关联是瞬时发生的,并不受时间和空间的限制。
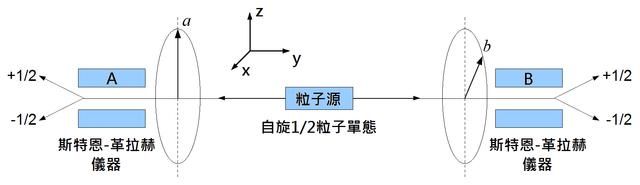
量子纠缠是由著名物理学家爱因斯坦、波多尔斯基和罗森在1935年提出来质疑量子力学完备性的一个思想实验。他们认为,如果量子力学是完备的,那么它应该能够描述所有的物理现象,包括量子纠缠。但是,量子力学却无法解释量子纠缠的机制,也无法预测量子纠缠的结果。他们认为,这是因为量子力学忽略了一些隐藏变量,即一些未被观测到的经典属性,来决定量子纠缠的行为。如果我们能够知道这些隐藏变量,那么我们就可以用经典物理学来描述量子纠缠,而不需要用量子力学。

贝尔不等式就是用来检验这个假设的一种数学工具。贝尔不等式是由贝尔在1964年提出的一种不等式关系,它用来限制隐藏变量理论对于量子纠缠的预测。贝尔不等式的基本思想是,如果存在隐藏变量,那么量子纠缠的结果应该满足一定的统计规律,即贝尔不等式;如果不存在隐藏变量,那么量子纠缠的结果应该违背贝尔不等式。因此,通过实验测量量子纠缠的结果,并与贝尔不等式进行比较,我们就可以判断是否存在隐藏变量。

贝尔不等式的具体形式有很多种,其中一种常见的形式是CHSH不等式,它由克劳泽、霍恩、希米尼和霍尔特在1969年提出的。CHSH不等式涉及到两个纠缠粒子A和B,以及两个测量装置X和Y。X和Y可以分别对A和B进行两种不同的测量,记为X1、X2和Y1、Y2。每次测量都会得到一个结果,记为+1或-1。CHSH不等式表明,如果存在隐藏变量,那么表达式的绝对值应该小于或等于2:
其中E表示期望值,即平均值。如果不存在隐藏变量,那么这个表达式的绝对值可以大于2,最大可以达到2根号2。
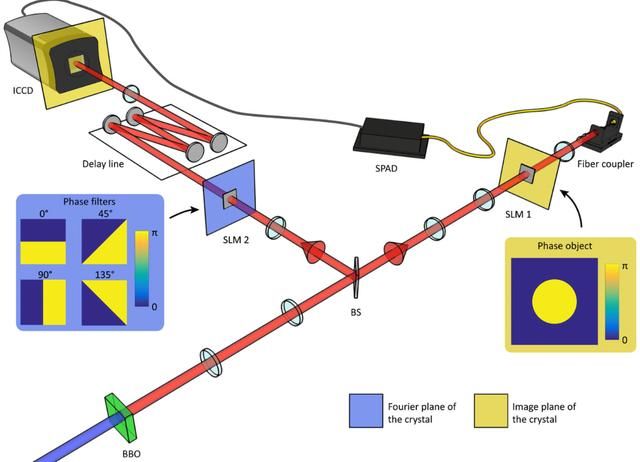
为了验证贝尔不等式是否成立,科学家们设计了一系列精密的实验。这些实验通常使用纠缠的光子或电子作为粒子对,并使用特殊的偏振器或磁场作为测量装置。实验中需要保证两个粒子之间没有任何物理联系,并且测量过程是随机和独立的。
最早的贝尔不等式实验是由弗里德曼和克劳泽在1972年进行的。他们使用了两个纠缠光子,并用偏振器来测量它们的偏振方向。他们发现了贝尔不等式被违背的证据,但是由于实验误差和效率问题,并没有得到决定性的结论。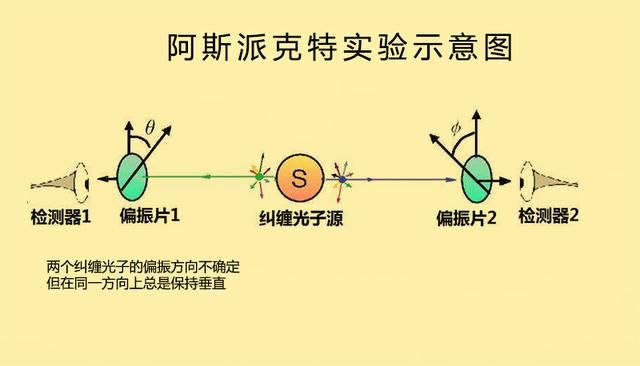 后来,随着技术的进步和实验条件的改善,更多更精确的贝尔不等式实验被进行。其中一个著名的实验是由阿斯佩克特、达利巴尔和罗杰在1982年进行的。他们使用了两个纠缠光子,并用快速开关来随机改变偏振器的方向。他们发现了贝尔不等式被违背的明显证据,这被认为是对量子纠缠的最强有力的实验验证。
后来,随着技术的进步和实验条件的改善,更多更精确的贝尔不等式实验被进行。其中一个著名的实验是由阿斯佩克特、达利巴尔和罗杰在1982年进行的。他们使用了两个纠缠光子,并用快速开关来随机改变偏振器的方向。他们发现了贝尔不等式被违背的明显证据,这被认为是对量子纠缠的最强有力的实验验证。
贝尔不等式的实验验证一直持续到现在,不断地消除各种可能的漏洞和误差。例如,有些人可能认为,两个粒子之间存在着一种未知的信号,来传递信息并影响测量结果。这种信号必须是超光速的,才能在瞬间跨越很远的距离。但是,根据相对论,超光速的信号是不可能存在的。为了排除这种可能性,科学家们使用了更远的距离和更快的开关来进行实验,确保两个粒子之间没有足够的时间来交换任何信号。结果仍然显示了贝尔不等式被违背的情况。

贝尔不等式的违背对物理学和其他领域产生了深远的影响。它表明,量子力学中的非局域性和不确定性是真实存在的,而不只是由于我们的测量限制。这一发现推动了对量子力学本质的深入研究,拓展了我们对自然界的理解。

贝尔不等式的研究还为量子信息科学和量子计算提供了新的可能性。量子信息科学是一门利用量子力学原理来处理和传输信息的科学,它涉及到量子通信、量子密码学和量子计算等领域。量子纠缠是量子信息科学中的一个重要资源,它可以实现一些经典信息科学无法实现或难以实现的功能。例如,通过利用量子纠缠,我们可以实现超密编码,即用一个纠缠光子来传输两比特(bit)的信息;或者实现量子隐形传态,即用两个纠缠光子来传输一个未知光子的状态;或者实现\tbr/>

量子计算是一种利用量子力学原理来进行计算的技术,它使用了一种叫做量子比特(qubit)的基本单元,来代替经典计算中的比特。量子比特可以同时处于0和1两种状态,而且可以与其他量子比特形成纠缠。这使得量子计算具有更高的并行性和灵活性,可以解决一些经典计算无法解决或难以解决的问题。例如,通过利用量子纠缠,我们可以实现Shor算法,即用量子计算来分解大整数;或者实现Grover算法,即用量子计算来搜索无序数据库;或者实现BQP复杂度类,即用量子计算来解决一些概率多项式时间内可解决但NP复杂度类内难以解决的问题。这些功能都可以提高我们的计算能力和速度。
贝尔不等式的发现也对我们对自由意志的理解产生了影响。一些学者认为,贝尔不等式的违背表明了物理世界的决定论性,即我们的行为可能受到量子纠缠的影响,而不完全由自由意志决定。他们认为,如果两个人之间存在着一种量子纠缠的联系,那么他们的选择可能是由这种联系决定的,而不是由他们自己的意愿决定的。这种观点引发了一些哲学和伦理上的争论,关于我们是否真正拥有自由意志,以及我们是否应该为我们的行为负责。
方豪胡4331数学基本不等式
屈冒梵13585982185 ______ (1的巧用) (1/x+1/y)*1=(1/x+1/y)(x+2y)=1+x/y+2y/x+2 =3+(x/y+2y/x)>=3+2 √ (x/y)*(2y/x)=3+2 √ 2
方豪胡4331数学基本不等式及其应用1
屈冒梵13585982185 ______ 1-3x-(2/x) =1-[3x+(2/x)] ∵x>0 ∴3x+(2/x)≥2√[3x*(2/x)]=2√6 ∴1-3x-(2/x)≤1-2√6 当3x=2/x即x=2√6/3时 原式取最大值1-2√6
方豪胡4331高二数学基本不等式
屈冒梵13585982185 ______ 首先把左边换成2分之2bc/a+2ac/b+2ab/c即为2分之(bc/a+ac/b)+2分之(bc/a+ab/c)+2分之(ac/b+ab/c). 由于在a,b大于0时有(a+b)/2大于等于根号ab,所以上面式子第一项大于等于√ (bc/a乘以ac/b)即为√ b的平方也就是b其他两项也是这样得到a和c
方豪胡4331指教 数学 基本不等式
屈冒梵13585982185 ______ 解:1.C lgx+lgy=lgxy 由基本不等式,得:2xy≤[½(2x+y)]^2=20/2=10 ∴xy≤50 原式≤lg50=lg5+lg10=1+lg5 即,lgx+lgy的最大值是1+lg5 失误!下面写对了,上面忘了带平方 第三行最后是100
方豪胡4331解基本不等式
屈冒梵13585982185 ______ 乙好.设前后两次粮价分别是a元/kg,b元/kg(a,b>0,a≠b).则综合两次购粮的平均粮价,甲是(a+b)/2元/kg,乙是2ab/(a+b)元/kg,甲-乙=[(a+b)/2]-[2ab/(a+b)]=(a-b)^2/[2(a+b)]>0.即综合购粮单价而言,甲比乙高,故乙的购粮方式更经济.
方豪胡4331数学基本不等式
屈冒梵13585982185 ______ 这个式子是由完全平方公式(m-n)^2=0得到的,也就是m^2+n^2=2mn,你的问题中a与这里的m^2对应,b与n^2对应,所以都必须大于或者等于0
方豪胡4331数学额 必修5 基本不等式最值
屈冒梵13585982185 ______ a=√2-1(b=√2)时,取得小值2√2 - 1 ab+b=2, b=2/(1+a) a+b=a+ 2/(1+a)=a+1 + 2/(a+1) -1 ≧2√[(a+1)* 2/(a+1)] - 1 = 2√2 - 1 (均值不等式:a>0, b>0, 则a+b≧2√ab;且,当a=b时“=”成立) 此处,当且仅当a+1=2/(a+1)成立时,即a=√2-1(b=√2)时,取得小值2√2 - 1
方豪胡4331基本不等式及其应用(要过程)
屈冒梵13585982185 ______ 4>=a+b>= 2√ab,所以1/√ab>=1/2 所以(a+b)/ab>=2√ab/ab=2/√ab>=1 选B
方豪胡4331基本不等式的运用步骤
屈冒梵13585982185 ______ 一正二定三相等 一正,即不等式中数为正数 二定,跟据不等号方向确定想要使用的基本不等式 三相等,确定基本不等式中取等号的条件能否满足
方豪胡4331数学基本不等式
屈冒梵13585982185 ______ 引用:A^2+B^2>=(A+B)^2/2 (展开,显然成立)所以原式左边》(a+1/a+b+1/b)^2/2=(1+1/ab)^2/2因为1=a+b>=2/ab所以ab<=1/4, 即1/ab>=4代入上式,即得证 证明:由柯西不等式:(1+1)[(a+1/a)^2+(b+1/b)^2]>=(a+1/a+b+1/b)^2=(1+1/a+1/b)^2 再用柯西不等式:(a+b)(1/a+1/b)>=(1+1)^2=4 所以1/a+1/b>=4 于是2[(a+1/a)^2+(b+1/b)^2]>=(1+4)^2=25 上式即(a+1/a)^2+(b+1/b)^2>=25/2