证明矩阵等价的方法

介绍

zk-SNARK，即“零知识简洁非交互式知识论证”，使得一名验证者 能够确认一名证明者 拥有某些特定知识，这些知识被称为 witness，满足特定的关系，而无需透露关于见证本身的任何信息。

为特定问题生成 zk-SNARK 包括以下四个阶段：

1. 将问题（或函数）转换成算术门电路。
2. 然后将这个电路翻译成矩阵公式。
3. 这个矩阵公式进一步转换成一个多项式，这个多项式应该能被一个特定的最小多项式整除。
4. 最后，这种可整除性在有限域的椭圆曲线点中表示出来，证明就在这里进行。

前三个步骤仅仅是转换了原始陈述的表示方式。最后一个步骤使用同态加密将第三步的陈述投影到加密空间中，使得证明者能够证实其中的镜像陈述。鉴于这种投影利用了非对称加密，从第三步的陈述回溯到原始陈述是不可行的，确保了零知识的暴露。

阅读本文所需的数学背景相当于 STEM 专业学生的大一级代数水平。唯一可能具有挑战性的概念可能是椭圆曲线加密。对于不熟悉这一点的人来说，可以将其视为具有特殊基数的指数函数，同时要记住其逆函数仍然未解。

本文将遵循以下符号规则：

• 矩阵：粗体大写字母，例如 ；显式形式写作
• 向量：带箭头的小写字母，例如；显式形式写作 ；默认情况下所有向量均为列向量
• 标量：常规字母表示

让我们用这个问题作为例子：

假设爱丽丝想要证明她知道一个 。我们将逐步介绍爱丽丝为她的证明生成 zk-SNARK 所需采取的整个程序。

这个问题可能看起来太简单，因为它不涉及控制流（例如，if-then-else）。然而，将带有控制流的函数转换为算术表达式并不困难。例如，让我们考虑以下问题（或在编程语言中的“函数”）：

f(x, z):

if(z==1):

return x*x*x+x*x+5

else:

return x*x+5

将这个问题重写为以下算术表达式很容易（假设 ），这并不比方程式 (1) 复杂多少。在本文中，我们将继续使用方程式 (1) 作为讨论的基础。

第1步：算术门电路

方程式 (1) 可以分解为以下基本算术运算：

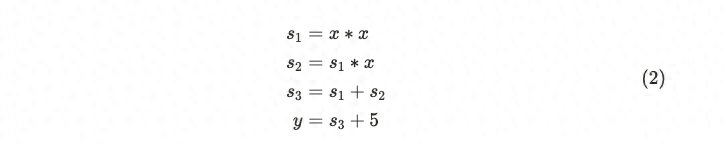
这对应于以下算术门电路：

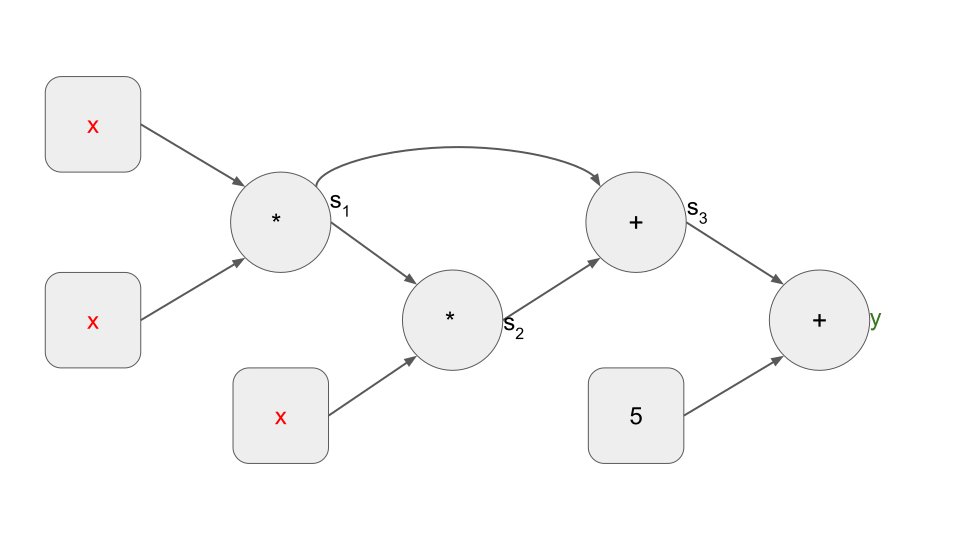
我们还将方程式 (2) 称为一组4个“一级约束”，每个约束描述了电路中一个算术门的关系。通常，一组 n 个一级约束可以概括为一个二次算术程序（QAP），接下来将进行解释。

第2步：矩阵

首先，让我们定义一个“见证”向量，如下所示：

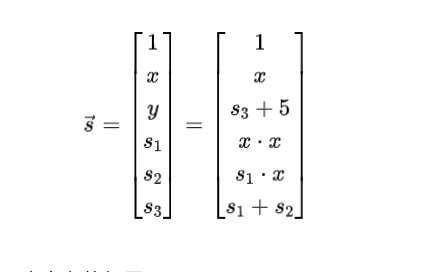
其中 与方程式 (2) 中定义的相同。

通常，对于一个有 个输入和 个算术门的问题（即 n-1 个中间步骤和最终输出），这个见证向量将是 维的。在实际问题中，数字 可能非常大。例如，对于哈希函数， 通常是几千。

接下来，让我们构造三个 n*(m+n+*1) 矩阵 ，以便我们可以将方程式 (2) 重写如下：

其中 表示逐点乘积，而且

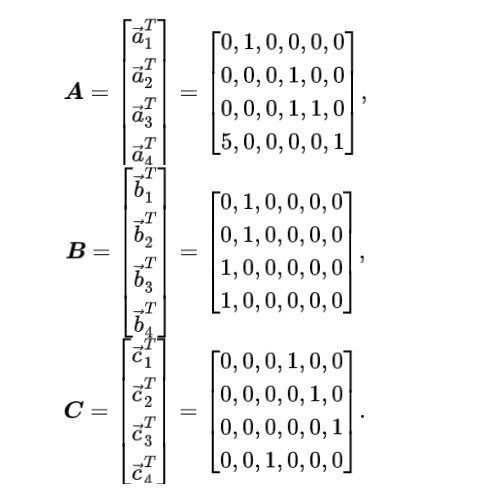
方程式 (3) 只是方程式 (2) 的另一种表示形式：每组 对应于电路中的一个门。我们只需要明确地展开矩阵公式就可以看到这一点：

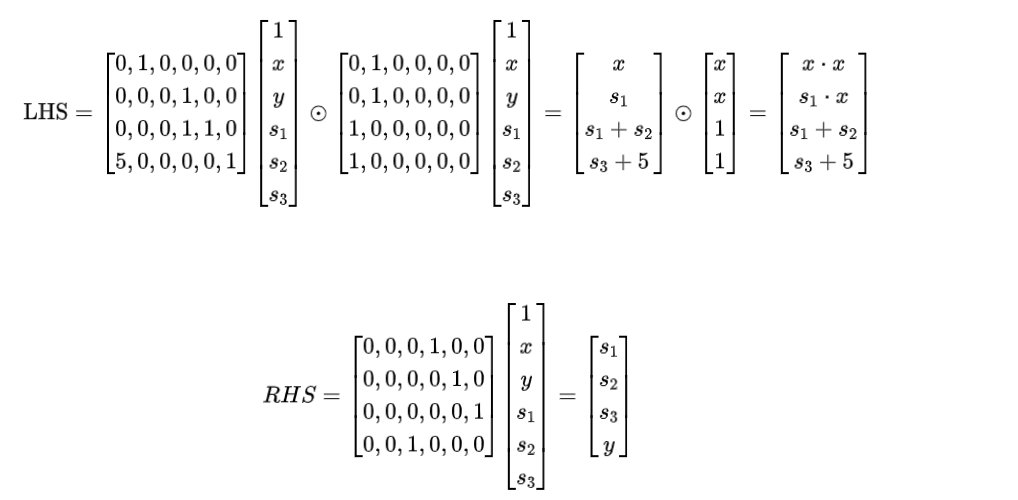
所以 与方程式 (2) 完全相同，矩阵方程的每一行对应一个一级约束（即电路中的一个算术门）。

我们跳过了构建 的步骤，其实这些步骤相对简单直接。我们只需要根据相应的一级约束，把它们转换成矩阵形式，从而确定 每一行的内容，即 。以第一行为例：可以很容易地看出，要使第一个一级约束 成立，我们需要的是将 、 和 与 相乘。

因此，我们已经成功地把算术门电路转换成了矩阵公式，即方程式 (3)。同时，我们也把需要证明掌握的对象，从 转变为了见证向量 。

第3步：多项式

现在，让我们构造一个 n*(*n+m+*1) 矩阵 ，它定义了一组关于 的多项式：

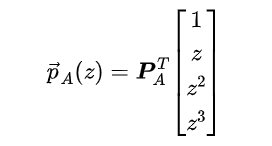
使得 在 {1,2,3,4}处的取值满足以下条件：

然后我们可以将 重写为：

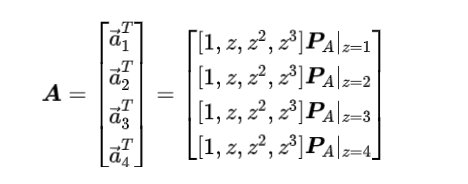
这些是六个变量的四组线性方程，可以用传统方法求解。然而，在这种情况下解决 的更有效方法是拉格朗日插值，它利用了问题的特殊性。这里我们跳过求解 的过程，虽然有点繁琐但很直接。

类似地，我们分别为 和 构造 和 。然后我们可以将矩阵公式 重写为：

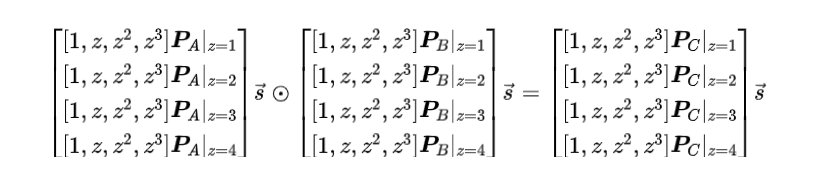
如果提取出每一行单独观察，不难发现这四行对应于在四个点分别求值的相同表达式。因此，上述矩阵方程等价于：

其中 定义为:

确定 在 是否成立的最快方法是检查它是否可以被 整除，这被称为“最小多项式”，记为 。即检查 的因式分解：是否存在一个多项式 使得 可以分解为 。换句话说，我们需要证明以下分解：

其中：

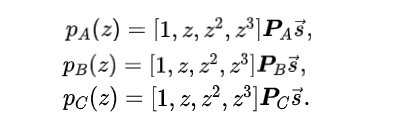
一种直接但不保密的方式来证明这一点是提供方程式 (4) 的左边并展示因式分解。然而，zk-SNARK 的主要目的是保持隐秘（不透露任何知识）。因此，我们不会直接证明这个方程，而是在椭圆曲线点的空间中证明它的加密版本。

第4步：椭圆曲线点

将方程式 (4) 重写为：

其中 只是 的一个平凡的零次多项式，用来使方程统一——所有项都是二次的。这样做的必要性很快就会变得清晰。注意这个方程只包含 的多项式的加法和乘法。

从高层次上看，这就是我们要做的：将多项式（具体来说，是多项式的系数）映射到椭圆曲线点，并将方程式 (5) 转换为加密空间中的以下镜像方程，这是需要证明的陈述：请注意，算术运算，加法 和乘法 ，也被映射到椭圆曲线点的有限域上的对应运算。圆圈中的运算符号 和 用来避免混淆，并表明这些是重新定义的域运算。

接下来，我们将更详细地阐述实际的操作步骤。

椭圆曲线加密

椭圆曲线的一般理论远远超出了本文的范围。就本文的目的而言，椭圆曲线被定义为从素域 的函数，其中 包括满足 的点（称为椭圆曲线点，简称 ECPs）。

请注意，虽然到目前为止我们一直在讨论常规算术，但现在当我们转换到素域时，数字的算术运算是以模运算的方式进行的。例如，，其中 是 的阶。

另一方面，两个椭圆曲线点的加法定义如下图所示：

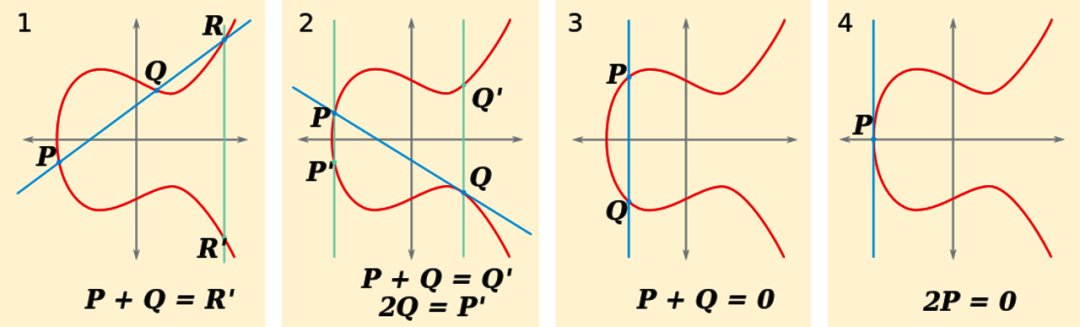
Figure from Wikipedia

具体来说，两个 ECPs 和 的加法：

1. 找到直线 和曲线的交点 ，定义为
2. 翻转到曲线上 的“镜像”点 。

因此我们定义椭圆曲线点的加法：

请注意，这个规则也适用于特殊情况，即一个 ECP 自加的情况，此时将使用该点的切线。

现在假设我们随机选择一个点 ，并将数字 映射到它上面。（这种“初始映射”听起来有点任意。稍后将进行讨论）。然后对于任何 ，我们定义：这有一个操作表达式。定义 的操作为“生成器”，记为 。那么上述定义等同于：也就是说， 是从 开始，进行 次 操作的椭圆曲线点。这实际上是椭圆曲线加密最初构建的方式：

1. 从 作为 开始；
2. 然后进行 操作跳转到 ：曲线和 处切线的交点的翻转；
3. 然后再次进行 操作跳转到 ：曲线和直线 的交点的翻转；
4. 依此类推。

所以 操作就像 中的 “++” 操作符。（请记住， 中的加法是以模运算的方式定义的）。

对于不熟悉椭圆曲线的人来说，你可以将这种映射类比为一个常规的指数函数，其中基数 代替了实数。算术运算的行为类似。然而，一个关键的区别是 的逆函数在计算上是不可行的。也就是说，没有办法计算椭圆曲线版本的 。这当然是椭圆曲线加密的基础。这样的映射被称为单向加密。

请注意，给定一个椭圆曲线，由于选择 （因此选择“生成器” ）是任意的（除了 x 轴上的点），有无限种映射方式。选择 （或 ）可以类比为选择指数函数的基数，这是常识的一部分。

定义了加法后，以下线性关系很容易看出：范数表达：因此， 中的任何线性关系（或约束）都会通过这种映射在加密空间 中得到保留。例如， 中的方程 将导致 ，或者 。

然而，Alice 想要证明的方程式 (5) 是二次形式的，所以线性不够。为了处理二次项，我们需要在加密空间中定义乘法。这被称为配对函数，或双线性映射，接下来将进行解释。

双线性映射

假设 和 是素数阶 的群。配对函数，或 双线性映射，定义为：

使得如果 分别是 和 的生成器，则 是 的生成器，并且 。

这个配对函数是我们在加密空间中需要的“乘法”操作，用于处理方程式 (5) 中的二次项。其中 是 和 中的元素。这个定义当然比本文所需的更为一般。你可以把 看作是椭圆曲线点。

让我们用 作为乘法操作的符号，那么双线性可以用算术形式重写：这是我们都熟悉的东西——加法和乘法操作的分配律。

有了这样的双线性映射，我们就可以将方程式 (5) 的两边映射到加密空间。

在这里，我们需要一个可信的第三方来选择五个随机系数：，以及一个随机点 ，在这个点上将会（虚拟地）评估多项式。这个 6 元组 被称为“toxic waste”，需要被丢弃。

请注意，整个程序基于对第三方正确处理有毒数据的信任。在现实中，这个“可信设置”程序并不是一个简单的任务。在这篇文章中，我们将假设这一步骤将被正确进行。

这整体被称为“证明钥”（proving key），记为 PK。请注意， 中包含向量的表示法应该被解释为椭圆曲线点的向量，其中每个点都是从相应的向量元素映射而来的。所以这 11 个向量实际上包含 62（=4*2+6*3+6*3+6*3）个椭圆曲线点。这 62 个 ECP 将被提供给 Alice，即证明者。在一个一般的情况下，对于一个有 个输入和 个一级约束的问题，PK 将包含 个 ECP。

同时，进行以下计算：

整个过程被称作“验证钥”，简称VK。这里只涉及7个椭圆曲线点（ECPs），需要提供给验证方。要注意的是，不管问题里面涉及多少输入和一级约束，VK始终是由7个ECPs构成的。

另外，值得一提的是，“可信设置”以及生成PK和VK的过程，对于一个特定的问题来说，只需操作一次即可。

现在拥有公钥（PK），爱丽丝将计算以下椭圆曲线点（ECPs）：

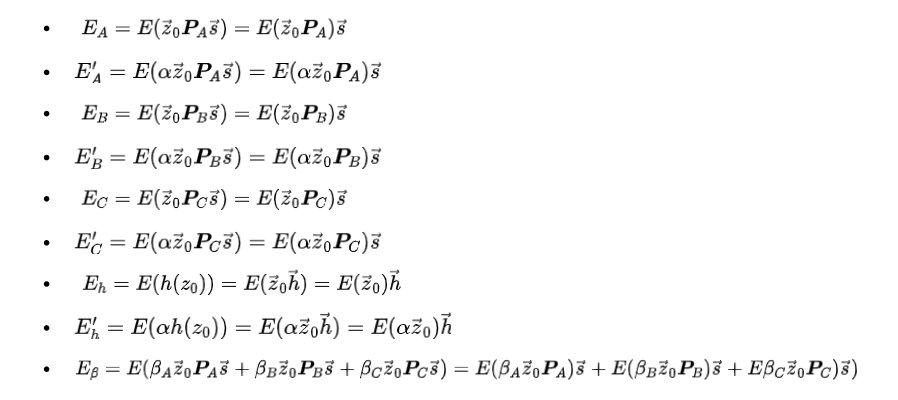
这9个椭圆曲线点就是零知识简洁非交互式证明（zk-SNARK）的关键！

注意，爱丽丝其实只是对公钥里的椭圆曲线点做了些线性组合运算。这点特别关键，验证时会重点检查。

现在，爱丽丝交出了zk-SNARK证明，咱们终于进入验证环节，分三步走。

首先得确认，前8个椭圆曲线点真的是通用参考串里那些点的线性组合。

其次，检查 确实来自同一个见证向量 ：

最后，检查等式（5）的相等性：

如果这三项检查都成立，那么等式（5）得到验证，因此我们相信爱丽丝知道见证。让我们解释一下等式背后的理由。以第一部分中的第一个等式为例，等式成立是因为双线性性质：然而，由于爱丽丝不知道 的值，她无法明确计算这个加法。她唯一能想出来满足等式的一对 的方法，是分别用相同的一组系数 ，计算 和 的两个组合。

杜霍孔633证明:m*n矩阵A和B等价<=>r(A)=r(B). -
扶贩振18220836185 ______ 设矩阵A,B等价,所以 存在可逆矩阵P,Q, 使得 B=PAQ 由于P可逆,因此,矩阵A与PA有相同的秩 而Q可逆,因此,矩阵PA与PAQ有相同的秩,即矩阵 A与B有相同的秩.这就证明了:m*n矩阵A和B等价=>r(A)=r(B).设 r(A)=r(B)=r 记C为如下的m*n矩阵,其左上角为一r阶单位矩阵,其它为0 Er 00 0.于是 存在可逆矩阵 P,Q使得 PAQ=C,同样 存在可逆矩阵 R,S使得 RBS=C.因此 PAQ=RBS B=R的逆*PAQ*S的逆,由于R的逆*P 与 Q*S的逆 都是可逆矩阵,于是 A与B等价.这就证明了:r(A)=r(B).=>矩阵A和B等价.

杜霍孔633两个矩阵等价的充分必要条件是什么? -
扶贩振18220836185 ______ 矩阵的秩相等,可经过初等变换来判断..

杜霍孔633N阶等价矩阵A、B的行列式绝对值是否相等?如题,应该是相等的,but如何合理地证明? -
扶贩振18220836185 ______[答案] B,则A、B的行列式相等,这明显是错的!是受老李的书的误导!很简单的反例:互换矩阵的两行,得到的矩阵与原矩阵等价吧,但是二者行列式可是不相等的,而是互为相反数哦!正确的结论应该是:两矩阵相似,则两矩阵的行列式相等.(因为...

杜霍孔633线性代数中,为什么说可逆矩阵等价于单位矩阵?最好给出一些证明或者简单的说明, -
扶贩振18220836185 ______[答案] 证:因为可逆矩阵是满秩矩阵,故它的等价标准形为 En. 即 A与单位矩阵等价. 注:任一矩阵A的等价标准形为 Er 0 0 0 其中 r 为A的秩.当A的秩 = n时,左上角的Er就成了En

杜霍孔633设A,B都是m*n阶矩阵,证明A与B等价的充要条件是A的秩等于B的秩. -
扶贩振18220836185 ______[答案] 如果A与B等价,则存在m阶可逆矩阵P,P1和n阶可逆矩阵Q,Q1使得B=PAQ,P1BQ1=P1PAQQ1= Ir 0 0 0 所以,A的秩等于B的秩. 反之,A的秩等于B的秩,则存在m阶可逆矩阵P1,P2和n阶可逆矩阵Q1,Q2使得P1BQ1=P2AQ2= Ir 0 0 0 令P=P1^(-1)P2,Q=...

杜霍孔633矩阵化简的方法或规律(例如化成矩阵的等价标准形或上(下)三角) -
扶贩振18220836185 ______ 把矩阵化为行最简形矩阵的方法 是指对矩阵做初等的行变换,将矩阵化为阶梯形.化简矩阵的目的是找到一个和原矩阵等价的,形式比较简单的矩阵,如上三角形,下三角形等.原矩阵和化简后的矩阵等价是指它们可以互相表出.这在求解线性方程组,求矩阵的秩,求矩阵的一个极大线性无关组等方面具有极大的便利. 化简的方法主要有: 1. 某一行乘以一个非零的常数; 2. 2.交换两行的位置; 3. 3.某一行减去另外一行和某个常数的积; 这些方法保证了矩阵的等价不变形. 4. 注意:化简矩阵具有灵活性,不同的人化简的结果也不同,但必须遵守两个原则:1.尽量使矩阵的形式简单,一般化为上三角形; 2.保持矩阵的等价性不变.

杜霍孔633线性代数如矩阵A,B等价,请问它们一定行等价,列等价吗?求证明过程 -
扶贩振18220836185 ______[答案] 这是不可能保证的. 注意定义: A和B等价:存在可逆阵P和Q使得B=PAQ A和B行等价:存在可逆阵P使得B=PA A和B列等价:存在可逆阵Q使得B=AQ 少掉一个矩阵就会少掉很多自由 比如说,A=[1,0],B=[0,1],显然是等价并且列等价的,但不是行等...

杜霍孔633关于矩阵等价的问题,看看证明错在哪.题目是:若A、B为等价矩阵,则A、B的行向量组等价.证明:因为R(A)=R(B)=R(A,B)=A行向量组的秩=B行向量组的秩 ... -
扶贩振18220836185 ______[答案] 矩阵等价的充要条件是 R(A)=R(B) 而不是 R(A)=R(B)=R(A,B) 这个等式是 A,B 列向量组等价的充要条件

杜霍孔633对于实n阶方阵A,B,C,试证明下列关系是等价关系(1)矩阵A,B等价,如果存在非奇异矩阵P,Q,使得B=PoAoQ; -
扶贩振18220836185 ______[答案] A=IAI,I是单位阵,所以A等价于A若A等价于B,则存在非奇异矩阵P,Q,使得B=PAQ非奇异矩阵P,Q有逆矩阵P1和Q1,所以P1BQ1=A,显然逆矩阵P1和Q1也是非奇异矩阵所以有B等价于A若A等价于B,B等价于C,则存在非奇异矩阵P,Q,T,S,使得...

杜霍孔633两个向量组如何等价?需要什么条件?
扶贩振18220836185 ______ 一般是先定义矩阵的等价.两个矩阵等价是指,一个矩阵经过初等变换能够变成另外一个矩阵(还可以细分为行等价(只用初等行变换)和列等价(只用初等列变换)).因为向量组可以组成矩阵,反过来矩阵又存在行向量组和列向量组,所以可以利用矩阵的等价来定义向量组的等价(只要把两个向量组都做成矩阵即可).一般定义向量组的等价,是用另外一个说法,就是“相互线性表示”.向量组A:a1,a2,...,am与向量组B:b1,b2,...,bk等价:向量组A中的每一个向量都可以由向量组B线性表示;向量组B中的每一个向量也可由向量组A线性表示.一般不讨论两个向量的等价,如果按照定义来理解的话,就是两个向量的元素对应成比例.